По математической логике и теории алгоритмов

для студентов 2 курса специальности

«Комплексная защита объектов информатизации»

Курск - 2005
ЛАБОРАТОРНАЯ РАБОТА № 1

ТЕМА: АЛГЕБРА ВЫСКАЗЫВАНИЙ.

ЦЕЛЬ:

1. Изучение основных понятий алгебры высказываний.

2. Освоение способов доказательств эквивалентности формул.

3. Изучение способов приведения формул к ДНФ, КНФ, СДНФ и СКНФ.

4. Изучение способов представления логических функций в виде многочлена Жегалкина.

ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ:

1. Определение высказывания. Требования, предъявляемые к высказываниям.
2. Понятие логической переменной.
3. Определение формулы алгебры логики.
4. Логические операции. Таблицы истинности для всех элементарных логических операций. Схема приоритета операций над формулами.
5. Понятие функции алгебры логики. Способы задания булевых функций.
6. Понятия пересечения, объединения и дополнения для булевых функций.
7. Понятие эквивалентности формул. Основные эквивалентности формул.
8. Понятие выполнимой, опровержимой, тождественно истинной, тождественно ложной формул.
9. Понятие ДНФ и КНФ. Алгоритм приведения формулы к ДНФ и КНФ.
10. Совершенный одночлен. Понятие СДНФ и СКНФ. Алгоритм приведения формул к СДНФ и СКНФ.
11. Алгоритм нахождения СДНФ и СКНФ формулы по известным таблицам истинности.
12. Понятие многочлена Жегалкина. Теорема Жегалкина.
13. Теорема Поста.

ЛИТЕРАТУРА:

1. В.Н. Нефедов, В.А. Осипова Курс дискретной математики. – М.: МАИ, 1992.–264 с.: ил.
2. О. П. Кузнецов, Г.М. Адельсон-Вельский Дискретная математика для инженера. – М.: Энергоатомиздат, 1988.– 480 с.: ил.
3. Ф.А. Новиков Дискретная математика для программистов.– СПб.: Питер, 2004.– 302 с.: ил.
4. С.В. Судоплатов, Е.В. Овчинникова Элементы дискретной математики: Учебник. – М.: ИНФРА-М; Новосибирск: НГТУ, 2003.– 280 с.
5. Гончарова Г.А., Мочалин А.А. Элементы дискретной математики. – М.:Форум-Инфра-М, 2004. – 128 с.
6. А.Н. Колмогоров, А.Г. Драгрлин Математическая логика. –М.: Едиториал УРСС, 2004. – 240 с.
7. Г.П. Гаврилов, А.А. Сапоженко Сборник задач по дискретной математике. –М.: Наука, 1977. – 368 с.

Краткая теория

Высказывание – повествовательное предложение, о котором в данном случае имеет смысл говорить истинно оно или ложно.

Поставим в соответствие высказыванию Р некоторую логическую переменную х, которая принимает значение 1, если Р – истинно и 0, если Р – ложно.

Если имеется несколько высказываний, то из них можно образовывать различные новые высказывания. При этом исходное высказывание называется простым, а вновь образованные высказывания – сложными высказываниями. Соответственно из логических переменных можно составлять различные конструкции, которые образуют формулы алгебры логики.

Пусть - множество логических переменных.

Тогда определим по индукции понятие формулы алгебры логики:

1) любая логическая переменная является формулой

2) если и - формулы, то формулами так же являются: , , , ,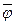

3) никаких других формул кроме построенных в п1) и п2) нет.

Символы Ø, ®, «,Ú,Ù - называются логическими связками или операциями.

Если формула построена из логических переменных {x₁, x₂, …x_n}то будем писать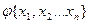

Действия логических операций задаются таблицами истинности, каждой строке которых взаимно однозначно ставятся набор значений переменных, составляющих формулу и соответствующее этому набору значение полученной формулы.

Введем следующие логические операции:

1) Штрих Шеффера - атиконъюнкция:

2) Стрелка Пирса 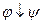- антидизъюнкция:

3) Кольцевая сумма - антиэквивалентность:

Функцией алгебры логики от n переменных {x₁, x₂, …x_n} называется любая функция 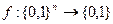то есть функция, которая произвольному набору нулей и единиц (d₁d₂…d_n) ставит в соответствие значение f(d₁d₂…d_n)Î{0,1}.

Такие функции еще называются булевыми функциями. Булева функция f(х₁х₂…х_n) полностью определяется своей таблицей истинности:

x1	x2	х3	…	xn-1	xn	f(х1х2…хn)
			…			f(0,0…0)
			…			f(0,0…1)
…	…	…	…	…	…	…
			…			f(1,1…0)
			…			f(1,1…1)

Если функция f(х₁х₂…х_n) и формула 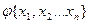имеют совпадающие таблицы истинности, то говорят, что формула 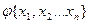представляет функцию f(х₁х₂…х_n).

Формулы 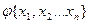и называются эквивалентными если совпадают их таблицы истинности, то есть совпадают представляемые ими функции и .

Дата добавления: 2017-02-01