Операции над предикатами

Пусть на множестве М заданы предикаты А(х) и В(х).

1. Будем считать, что 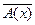так же определяет предикат на множестве М, причем при каждом фиксированном х = а, значение высказывания 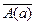противоположно значению высказывания А(х).

2. Аналогично из предикатов А(х) и В(х) с помощью логических связок Ù,Ú,®, ↔ можно образовывать предикаты А(х)ÙВ(х), А(х)ÚВ(х), А(х)®В(х), А(х)↔В(х).

3. Кроме операций логики высказываний будем применять к предикатам операции связывания кванторами.

Пусть М – предметное множество, Р(х) – одноместный предикат на множестве М. Тогда введем следующие кванторы действия:

1) 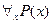- читается «для любого х имеет место Р(х)», «для всех х х имеет место Р(х)», «для каждого х выполняется Р(х)».

Под выражением 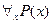будем подразумевать высказывание, которое истинно когда Р(х) – истинно для каждого х ÎМ и ложно в противном случае.

Символ 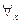называется квантором всеобщности.

2) 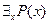- читается «существует х для которого Р(х)», «для некоторых х выполняется Р(х)», «хотя бы для одного х выполняется Р(х)».

Под выражением 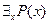будем понимать высказывание, которое истинно, если Р(х) принимает значение «истина» хотя бы для одного значения х, и ложно, если Р(х) – ложно для всех переменных х ÎМ. Символ 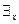называется квантором существования.

Пример решения задачи 1

Задача: Ниже приведена легенда. Запишите с использованием 4-6 различных букв формулу или теорему, отвечающее тексту или контексту легенды, для чего сформулируйте необходимые посылки и два следствия: одно истинное, а другое ложное.

«В эти брезентовые штаны не пытайся влезть – в них ты смотришься как маляр». – «Но и это шерстяное платье я тоже не надену – оно на мне как на вешалке». – «Как на счет кожаного пиджака и юбки с разрезом?» - «У юбки заело молнию, а пиджак вот здесь испачкан». – «Ну, это не беда; пятно прикроется сумкой». – «Да, пожалуй, ты права – сумку в любом случае надо брать; она очень идет к моим любимым туфлям». – «Сломанную молнию заменит булавка, а ее прикроет пиджак». – «Хорошо, так и сделаем».

Решение:

Пусть имеет следующие высказывания:

А – Надеть брезентовые штаны

В – Надеть шерстяное платье

С – надеть пиджак и юбку

D – Взять с собой сумку

Е – Великолепно смотрится

«Я смогу надеть на себя или брезентовые штаны или шерстяное платье или пиджак и юбку с разрезом» = (А Ú В Ú С).

«Я буду выглядеть великолепно, если надену пиджак и юбку с разрезом и при этом возьму с собой сумку» = ((С Ù D) ® Е)

«Я буду выглядеть ужасно, если надену на себя брезентовые штаны или шерстяное платье» = ((АÚВ)® ).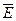

Однако «сумку надо брать обязательно, если надеть пиджак и юбку с разрезом» = (С® D).

Итак, «чтобы выглядеть великолепно, я надену на себя пиджак и юбку с разрезом» = (С ® Е). Это заключение является истинным.

Тогда полная теорема, соответствующая контексту данного диалога будет иметь вид:

А Ú В Ú С; (С Ù D) ® Е; (АÚВ)® 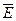; С® D Þ С ® Е.

Вариант 1

Задача 1

Ниже приведена легенда. Запишите с использованием 4-6 различных букв формулу или теорему, отвечающее тексту или контексту легенды, для чего сформулируйте необходимые посылки и два следствия: одно истинное, а другое ложное.

«Ваня и Петя – близнецы. Ваня с огромной скоростью улетел в космос на ракете, а Петя остался на неподвижной Земле. Теория относительности утверждает, что если лететь на большой скорости, то время замедляется, поэтому Петя состариться, а Ваня – нет. Эта же теория учит, что движение относительно: если Ваня движется относительно Пети, то и Петя движется относительно Вани. Однако по теории почему-то именно Ваня, вернувшись из полета, будет моложе Пети. Вывод: теория относительности не свободна от противоречий».

Задача 2

Докажите выводимость в ИВ: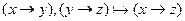

Задача 3

С помощью алгоритма Квайна проверить общезначимость формулы:

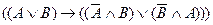
Задача 4

С помощью алгоритма редукции проверить общезначимость формулы:

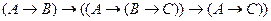
Задача 5

Введем следующие обозначения: Z(x, t) – я вижу предмет х в момент времени t; P(x, t) – я беру предмет х в момент времени t; Q(t^* , t) – момент времени t^* предшествует моменту времени t. Напишите, используя эти обозначения, символические выражения для следующих предложений:

1) Я всегда что-то вижу.

2) Перед тем как я беру предмет, я вижу его.

3) Некоторые вещи, которые я видел ранее, я всегда вижу вновь спустя определенное время.

Задача 6

Доказать общезначимость формул:

1)

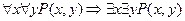
2)

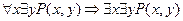
Вариант 2

Задача 1

Ниже приведена легенда. Запишите с использованием 4-6 различных букв формулу или теорему, отвечающее тексту или контексту легенды, для чего сформулируйте необходимые посылки и два следствия: одно истинное, а другое ложное.

«Уменьшение температуры приводит к снижению давления и уменьшению объема. Увеличение объема приводит к росту скорости потока. Повышение давления приводит к падению уровня, если при этом уменьшать температуру. Снижение скорости приводит к уменьшению давления и росту температуры. Технолог Иванов рассудил так: «Мне надо повысить давление при одновременном снижении скорости потока, поэтому я должен увеличить объем и температуру»».

Задача 2

Докажите выводимость в ИВ: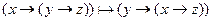

Задача 3

С помощью алгоритма Квайна проверить общезначимость формулы:

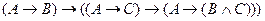
Задача 4

С помощью алгоритма редукции проверить общезначимость формулы:

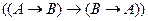
Задача 5

Введем следующие обозначения: Z(x, t) – я вижу предмет х в момент времени t; P(x,t) – я беру предмет х в момент времени t; Q(t^* , t) – момент времени t^* предшествует моменту времени t. Напишите, используя эти обозначения, символические выражения для следующих предложений:

1) Иногда я ничего не вижу.

2) Всегда существуют вещи, которые я не вижу и не беру.

3) Я беру всякий предмет, который я еще не взял до этого.

Задача 6

Доказать общезначимость формул:

1)

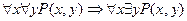
2)

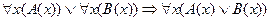
Вариант 3

Задача 1

Ниже приведена легенда. Запишите с использованием 4-6 различных букв формулу или теорему, отвечающее тексту или контексту легенды, для чего сформулируйте необходимые посылки и два следствия: одно истинное, а другое ложное.

«Если усложнить схему устройства, то возрастет его производительность, а если использовать новую элементную базу, то увеличиться период эксплуатации. Устройство начнут хорошо раскупать только при одновременном росте его производительности и периоде эксплуатации. Но устройство не пользуется спросом».

Задача 2

Докажите выводимость в ИВ: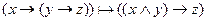

Задача 3

С помощью алгоритма Квайна проверить общезначимость формулы:

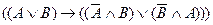
Задача 4

С помощью алгоритма редукции проверить общезначимость формулы: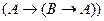

Задача 5

Введем следующие обозначения: Z(x, t) – я вижу предмет х в момент времени t; P(x, t) – я беру предмет х в момент времени t; Q(t^* , t) – момент времени t^* предшествует моменту времени t. Напишите, используя эти обозначения, символические выражения для следующих предложений:

1) Существуют предметы, которые я никогда не вижу.

2) Я всегда вижу либо все, либо ничего.

3) Я никогда не беру того, что я всегда вижу.

Задача 6

Доказать общезначимость формул:

1)

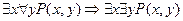
2)

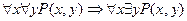
Вариант 4

Задача 1

Ниже приведена легенда. Запишите с использованием 4-6 различных букв формулу или теорему, отвечающее тексту или контексту легенды, для чего сформулируйте необходимые посылки и два следствия: одно истинное, а другое ложное.

«Любой марксист – диалектик, но не всякий диалектик – марксист. Любой марксист – материалист, но не всякий материалист – марксист. Гегель был диалектик, но не материалист. Фейербах был материалист, но не диалектик. Итак, если бы Гегель и Фейербах могли объединиться в один кружек, то Маркс уже не понадобился бы».

Задача 2

Докажите выводимость в ИВ: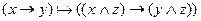

Задача 3

С помощью алгоритма Квайна проверить общезначимость формулы:

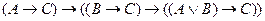
Задача 4

С помощью алгоритма редукции проверить общезначимость формулы:

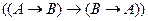
Задача 5

Введем следующие обозначения: Z(x, t) – я вижу предмет х в момент времени t; P(x, t) – я беру предмет х в момент времени t; Q(t^* , t) – момент времени t^* предшествует моменту времени t. Напишите, используя эти обозначения, символические выражения для следующих предложений:

1) Я вижу каждую вещь в некоторый момент времени.

2) Не существует предметов, которые я никогда не беру.

3) Если я беру предмет, не видя его до этого, то через некоторое время я вижу его, но не беру.

Задача 6

Доказать общезначимость формул:

1)

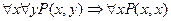
2)

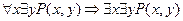
Вариант 5

Задача 1

Ниже приведена легенда. Запишите с использованием 4-6 различных букв формулу или теорему, отвечающее тексту или контексту легенды, для чего сформулируйте необходимые посылки и два следствия: одно истинное, а другое ложное.

«Если в цепи будет большой перепад напряжения, то сгорит предохранитель, что повлечет за собой необходимость его замены. При целом предохранителе телевизор, конечно, будет работать, но только если его включить в сеть питания. Если телевизор работает нормально, то я увижу сегодняшние «Новости». Итак, я смотрю телевизионные новости при условии отсутствия перепада напряжения и подключения телевизора к сети питания».

Задача 2

Докажите выводимость в ИВ: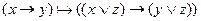

Задача 3

С помощью алгоритма Квайна проверить общезначимость формулы:

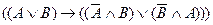
Задача 4

С помощью алгоритма редукции проверить общезначимость формулы:

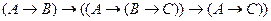
Задача 5

Введем следующие обозначения: Z(x, t) – я вижу предмет х в момент времени t; P(x, t) – я беру предмет х в момент времени t; Q(t^* , t) – момент времени t^* предшествует моменту времени t. Напишите, используя эти обозначения, символические выражения для следующих предложений:

1) Если я вижу предмет, то я тут же его беру.

2) Я никогда не беру того, что я всегда вижу.

3) Я беру всякую вещь, которую я никогда не вижу.

Задача 6

Доказать общезначимость формул:

1)

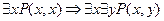
2)

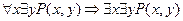
Дата добавления: 2017-02-01