Лабораторная работа № 4

ТЕМА: ТЕОРИЯ АЛГОРИТМОВ. МАШИНЫ ТЬЮРИНГА.

ЦЕЛЬ:

5. Изучение основных понятий теории алгоритмов.

6. Изучение принципов построения и работы машины Тьюринга.

ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ:

1. Интуитивное понятие алгоритма.

2. Свойства алгоритмов.

3. Конструктивное определение машины Тьюринга.

4. Программа. Свойства программы машины Тьюринга.

5. Способы задания машины Тьюринга.

6. Понятие текущей конфигурации машины Тьюринга. Начальная и заключительная конфигурации.

7. Понятие применимости машины к данной конфигурации.

8. Определение функции правильно вычислимой по Тьюрингу.

ЛИТЕРАТУРА:

1. О. П. Кузнецов, Г.М. Адельсон-Вельский Дискретная математика для инженера. – М.: Энергоатомиздат, 1988.– 480 с.: ил.
2. С.В. Судоплатов, Е.В. Овчинникова Элементы дискретной математики: Учебник. – М.: ИНФРА-М; Новосибирск: НГТУ, 2003.– 280 с.
3. Гончарова Г.А., Мочалин А.А. Элементы дискретной математики. – М.:Форум-Инфра-М, 2004. – 128 с.
4. А.Н. Колмогоров, А.Г. Драгрлин Математическая логика. –М.: Едиториал УРСС, 2004. – 240 с.
5. Г.П. Гаврилов, А.А. Сапоженко Сборник задач по дискретной математике. –М.: Наука, 1977. – 368 с.

Краткая теория

Понятие алгоритма принадлежит к числу основных понятий математики. Под алгоритмом понимают точное предписание о выполнении в определённом порядке системы операций для решения всех задач некоторого данного типа.

Простейшими алгоритмами являются правила, по которым выполняется та или иная из четырёх алгоритмических операций.

Т.е. если говорить неформально, то алгоритм - это детерминированная процедура, которую можно применять к любому элементу некоторого класса символьных входов и которая для каждого такого входа даёт, через конечное число действий соответствующий символьный выход.

Существенными чертами неформального понятия алгоритма являются следующие:

1. алгоритм задаётся как набор инструкций конечных размеров, т. е. его можно вписать конечным набором слов и специальных символов.

2. имеется вычислитель, обычно человек, который умеет обращаться с инструкциями и производить вычисления.

3. алгоритм имеет некоторое число входных данных.

4. имеется возможность для выделения, запоминания и повторений шагов вычислений.

5. для каждого данного входа вычисление производится по данным инструкциям.

с помощью алгоритма получается одно или нескольких данных.

Все задачи математике разделить на два класса: задачи для которых найдены алгоритмы решения и задачи для которых алгоритмы ещё не найдены. С развитием математической логики обнаружили ещё третий класс так называемых «алгоритмически неразрешимых задач» - задач для которых построение алгоритма невозможно.

Дадим математическое описание алгоритма и его свойств.

Алфавитом будем называть некоторое непустое множество А, а сами символы алфавита будем называть буквами:

А ={ а, б, +,–,?...}

Словом в данном алфавите А называют всякую конечную последовательность букв алфавита. Причём пустая последовательность букв называется пустым словом и обозначается α_0.

Чем P– слово (а в в) и Q – слово (d d), то пусть PQ обозначает слово (a b b d d).

Тогда верно, что для любого слова P выполняется …P=P…=P.

Алфавит А называется расширением алфавита В, если ВСА. Чем алфавит А есть расширение алфавита В, то всякое слово алфавита В является словом и в алфавите А.

Будем говорить, что слово R входит в слово Q если Q=R R R, где R R – любые, может быть и пустые слова. Слово R может входить в Q несколько раз, и первымвхождением будем считать самое левое вхождение в записи Q.

Под алгоритмом в алфавите А понимаем алгоритм, входами и выходами которого являются слова алфавита А. Алгоритм обозначается заглавными латинскими буквами (M, N,S …).

Пусть Р – слово алфавита А. Говорят, что алгоритм N применим к слову Р, если применение его к Р приводит, через конечное число шагов к некоторому слову Q алфавита А. При этом записывают Q=N(P). Чем процесс преобразования слова Р бесконечное, то считается, что алгоритм не применим к этому слову.

Свойства алгоритмов.

1. Дискретность – процесс нахождения решения происходит отдельными шагами, при этом подразумевается, что данные получаемые на следующем шаге получаются из уже найденных по данному закону.

2. Детерминированность – данные получаемые на каждом шаге однозначно определяются данными предшествующих шагов.

3. Элементарность – правила получения данных на каждом шаге однозначно определяются данными предшествующих шагов.

4. Направленность – если на каком – то шаге правила получения данных не дают результата, то должно быть точно указано, что в данном случае считать за результат.

5. Массовость – начальная система данных может быть выбрана из некоторого бесконечного множества.

Можно выделить 3 типа алгоритмов

1) Программы – нормальные алгоритмы Маркова

2) Исполнители – машины Тьюринга, Пьста, Минского

3) Функции – рекурсивные функции, 2 – определённые функции.

Машина Тьюринга состоит из следующих элементов:

1) Ленты разбитой на ячейки и бесконечной в обе стороны.

В каждой ячейке ленты можно записать один символ конечного алфавита A={a₀ a₁…a_m}, который называется внешним алфавитом. Символ a₀ принято считать пустым символом.

2)Управляющего устройства, которое может находиться в одном из конечного числа внутренних состояний Q={q₀q₁…q_n}. Число элементов в Q характеризует объем внутренней памяти машины. В множестве всех внутренних состояний Q выделяют два состояния q₀ – начальное состояние, которым обладает всякая машина, q₁ – заключительное состояние, попав в которое машина останавливается.

3) Считывающей головки, которая может перемещаться вдоль ленты в каждый момент времени обозревать (считывать) одну из ячеек ленты.

Работа машины происходит в дискретные моменты времени t = 0,1,2…

В зависимости от внутреннего состояния машины работа машины заключается в следующем:

1) Находясь в состоянии g_i и обозревая a_i, головка может затереть символ a_i и записать в обозреваемую ячейку символ a_l и перейти в следующие внутреннее состояние g_k. Символическая запись: g_i a_{j →}a_l g_k d где d = {L,R,E}- показывает направление движения головки.

2) Находясь в состоянии g_i и обозревая символ a_i головка может сдвинуться на одну ячейку влево и перейти в состояние g_k. Символически: g_i a_{j →L} g_k.

3) Находясь в состоянии g_i и обозревая символ a_j головка может сдвинуться на одну ячейку вправо и перейти в состояние g_к .Символически: g_i a_{j →} R g_k.

Любая машина Тьюринга имеет конечное (непустое) множество команд, которое называется программой машины (Р). При этом должны выполниться следующие условия:

1)Р не содержит команд с одинаковой левой частью

2) В Р обязательно присутствует команда левая часть которой содержит начальное состояние g₁.

Машина останавливается, если она находится в некотором внутреннем состоянии g_1, обозревает символ a_k и среди команд нет команды, начинающийся с g_j a_k.

Программа машины Тьюринга может быть задана тремя основными способами:

1)Системой правил – программа.

2) Таблицей – строкам которой соответствуют внутренние состояния, а столбцам символы внешнего алфавита. На пересечении строк и столбцов записывается правая часть команда. Например, для команды g_i a_{j →} a_n g_m таблица будет иметь вид:

3) Блок – схемой или графом переходов. На данном графе вершинами являются внутренние состояния машины, а ребра показывают под действием, какого внешнего символа, какой внешний символ записывается.

Если на ленте имеется слово А, читающая головка помещена на квадрат с первой буквой этого лова и машина приведена во внутренние состояние g₀ , то машина начинает свою работу на ленте в соответствии с программой.

Если при этом машина когда –нибудь останавливается, то находящиеся в момент остановки слово на ленте считается результатом применения машины Т к слову А. (обозначается Т(А)).

Если процесс работы машины Т для данного слова А бесконечен, то говорят, что машина Т неприменима к слову А.

Под текущей конфигурацией (К) машины Тьюринга понимается совокупность состояний ленты, внутреннего состояния машины и символа, обозреваемого головкой.

Обозначается: К = а_i1 а_i2…..a_ik a_ik+1 …..a_ik+l

где a_i1 – крайний слева не пустой символ

a_ik+l – крайний справа не пустой символ

a_ik+1 – символ в обозреваемой ячейке

Более коротко это можно записать так: λ g_i a_i β где

λ – последовательность символов слева от а_i

β – последовательность символов справа от а_i

Причем на каждом шаге работы конфигурация машины меняется, конфигурация из которой машина начинает работу λ g₀ a_i β называется начальной, а конфигурация в которой машина заканчивает работу λ₁ g₁ a_n β₁- конечной.

Условимся что конфигурация К называется заключительной, если g_i = g₁

Стандартная начальная конфигурация имеет вид g₀ λ, а стандартная заключительная λ g_1. конфигурацию в момент времени t обозначают K_t.

Если К₀ = g_{i λ} и λ = а_i λ и а_i € А, то программе машины имеется точно одна команда вида g₀ аi – а_l g_k d, где d показывает направление движение головки. Тогда следующая конфигурация К₁ определяется так:

К₁ = g _k а_l λ если d = Е

К₁ = а_l g _k λ если d = R

К₁ = g _k а₀ а_l λ если d = L

Такой переход обозначают К₀ – К₁ и если К₁ не является заключительной, то в соответствии с системой команд аналогично однозначно определима следующая конфигурация К₂ и т.д.

К₀ – К₁ - К₂ - …- К_t - К_t+1 … -

Если данная последовательность является конечной, то говорят, что машина применима к конфигурации К₀ , в противном случае неприменима к К_0.

Определим вычисления функций на машине Тьюринга.

Будем рассматривать словарные функции f: А* - А*, где А* - множество всех слов алфавита А имеющих конечную длину.

Говорят, что машина Тьюринга правильно вычисляет частичную функцию f если для любого слова р € А* выполняются условия:

1) если f (р) определено и f(р) = r, то машина Тьюринга применима к начальной конфигурации К₀ = g₀ р и заключительной является конфигурация К_t = g₁r.

2) если f(р) не определено, то машина Тьюринга неприменима к начальной конфигурации g₀ р.

При этом функция f называется правильно вычислимой по Тьюрингу, если существует машина Тьюринга, которая ее правильно вычисляет.

Аналогичные определения можно дать и для функций нескольких переменных. Для этого множество слов, являющихся аргументами записывают в виде одного слова ввода знак - разделитель *.

Пусть имеем функцию f(x₁ x₂….x_n) аргументы и значений которой принадлежит множеству N. Будем считать что алфавит А машины Тьюринга содержит 1. Произвольное число x € N будем представлять в виде слов 1^x+1 = | 1…1| и таким образом запись нуля не будет пустой.

Тогда будем говорить что машина Тьюринга правильно вычисляет функцию f(x₁ x₂….x_n) если:

1) если значение функции f (х_1…….х_n) определено, то конфигурацию

g₀ |1_…..1|*|1_……1|*_……..*|1_…….1| она переводит в конфигурацию g₁ |1_…….1|

2) если значение функции f (х_1…….х_n) неопределенно, то Т не применима к данной функции.

Здесь знак *-символ-разделитель из алфавита А.

Вариант 1

Задача 1

Машина Тьюринга задана следующими командами:

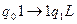
На ленте записано слово 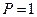, и читающая головка находится над этим словом во внутреннем состоянии 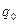. Опишите работу машины и постройте граф состояний.

Задача 2

Машина Тьюринга с начальной конфигурацией 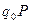и внешним алфавитом задана следующим набором команд:

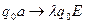
Опишите работу данной машины, постройте граф ее внутренних состояний и проверьте, применима ли данная машина к конфигурации .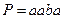

Задача 3

Пусть . Построить машину Тьюринга (записать последовательность команд и дать описание ее работы), которая любое число n в десятичной записи перерабатывала бы в число n – 1.

Задача 4

Построить машину Тьюринга, которая бы справа от любого слова Р в алфавите приписывала бы слово 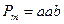. Описать работу данной машины и построить граф ее внутренних состояний.

Задача 5^*

Постройте машину Тьюринга для умножения чисел на 2.

Вариант 2

Задача 1

Машина Тьюринга задана следующими командами:

На ленте записано слово 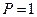, и читающая головка находится над этим словом во внутреннем состоянии 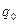. Опишите работу машины и постройте граф состояний.

Задача 2

Машина Тьюринга с начальной конфигурацией 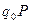и внешним алфавитом задана следующим набором команд:

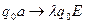
Опишите работу данной машины, постройте граф ее внутренних состояний и проверьте, применима ли данная машина к конфигурации .

Задача 3

Пусть . Построить машину Тьюринга (записать последовательность команд и дать описание ее работы), которая любое число n в десятичной записи перерабатывала бы в число n + 1.

Задача 4

Построить машину Тьюринга, которая бы слева от любого слова Р в алфавите приписывала бы слово . Описать работу данной машины и построить граф ее внутренних состояний.

Задача 5^*

Постройте машину Тьюринга для умножения чисел на 2.

Вариант 3

Задача 1

Машина Тьюринга задана следующими командами:

На ленте записано слово 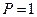, и читающая головка находится над этим словом во внутреннем состоянии 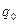. Опишите работу машины и постройте граф состояний.

Задача 2

Машина Тьюринга с начальной конфигурацией 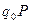и внешним алфавитом задана следующим набором команд:

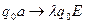
Опишите работу данной машины, постройте граф ее внутренних состояний и проверьте, применима ли данная машина к конфигурации .

Задача 3

Пусть . Построить машину Тьюринга (записать последовательность команд и дать описание ее работы), которая любое число n в десятичной записи перерабатывала бы в число n + 2.

Задача 4

Построить машину Тьюринга, которая бы справа от любого слова Р в алфавите приписывала бы слово 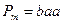. Описать работу данной машины и построить граф ее внутренних состояний.

Задача 5^*

Постройте машину Тьюринга для умножения чисел на 2.

Вариант 4

Задача 1

Машина Тьюринга задана следующими командами:

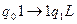
На ленте записано слово 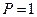, и читающая головка находится над этим словом во внутреннем состоянии 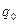. Опишите работу машины и постройте граф состояний.

Задача 2

Машина Тьюринга с начальной конфигурацией 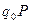и внешним алфавитом задана следующим набором команд:

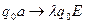
Опишите работу данной машины, постройте граф ее внутренних состояний и проверьте, применима ли данная машина к конфигурации .

Задача 3

Пусть . Построить машину Тьюринга (записать последовательность команд и дать описание ее работы), которая любое число n в десятичной записи перерабатывала бы в ноль.

Задача 4

Построить машину Тьюринга, которая бы слева от любого слова Р в алфавите приписывала бы слово 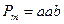. Описать работу данной машины и построить граф ее внутренних состояний.

Задача 5^*

Постройте машину Тьюринга для умножения чисел на 2.

Вариант 5

Задача 1

Машина Тьюринга задана следующими командами:

На ленте записано слово 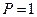, и читающая головка находится над этим словом во внутреннем состоянии 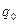. Опишите работу машины и постройте граф состояний.

Задача 2

Машина Тьюринга с начальной конфигурацией 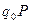и внешним алфавитом задана следующим набором команд:

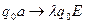
Опишите работу данной машины, постройте граф ее внутренних состояний и проверьте, применима ли данная машина к конфигурации .

Задача 3

Пусть . Построить машину Тьюринга (записать последовательность команд и дать описание ее работы), которая любое число n в десятичной записи перерабатывала бы в число n + 2.

Задача 4

Построить машину Тьюринга, которая бы справа от любого слова Р в алфавите приписывала бы слово . Описать работу данной машины и построить граф ее внутренних состояний.

Задача 5^*

Постройте машину Тьюринга для умножения чисел на 2.

Дата добавления: 2017-02-01