Лабораторная работа № 3

ТЕМА: ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ. ЛОГИКА ПРЕДИКАТОВ.

ЦЕЛЬ:

3. Изучение методов доказательства выводимости и общезначимости формул исчисления высказываний: алгоритм Квайна и метод редукции.

4. Изучение методов построения логических выражений с использованием предикатов.

ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ:

1. Понятие формальной аксиоматической теории.

2. Определение теоремы исчисления высказываний (ИВ).

3. Определение множества формул ИВ.

4. Правило вывода в ИВ.

5. Алгоритмы проверки общезначимости формул ИВ.

6. Понятие предиката: одноместный и к -местный предикаты.

7. Операции над предикатами.

8. Кванторы существования и всеобщности, связные и свободные переменные, область действия квантора.

9. Понятие формулы логики предикатов.

10. Правила образования формул. Равносильность формул.

11. Правила перехода к равносильным в любой интерпретации формулам.

12. Исчисление предикатов: аксиомы и правила вывода, доказательство общезначимости формул исчисления предикатов.

ЛИТЕРАТУРА:

1. В.Н. Нефедов, В.А. Осипова Курс дискретной математики. – М.: МАИ, 1992.–264 с.: ил.
2. О. П. Кузнецов, Г.М. Адельсон-Вельский Дискретная математика для инженера. – М.: Энергоатомиздат, 1988.– 480 с.: ил.
3. Ф.А. Новиков Дискретная математика для программистов.– СПб.: Питер, 2004.– 302 с.: ил.
4. С.В. Судоплатов, Е.В. Овчинникова Элементы дискретной математики: Учебник. – М.: ИНФРА-М; Новосибирск: НГТУ, 2003.– 280 с.
5. Гончарова Г.А., Мочалин А.А. Элементы дискретной математики. – М.:Форум-Инфра-М, 2004. – 128 с.
6. А.Н. Колмогоров, А.Г. Драгрлин Математическая логика. –М.: Едиториал УРСС, 2004. – 240 с.
7. Г.П. Гаврилов, А.А. Сапоженко Сборник задач по дискретной математике. –М.: Наука, 1977. – 368 с.

Краткая теория

Формальная аксиоматическая теория (формальное исчисление) считается заданной, если выполняются следующие условия:

1. Имеется некоторое множество символов А – алфавит исчисления. Конечные последовательности символов из множества А называются словами или выражениями исчисления I. Множество всех слов алфавита исчисления I обозначается S.

2. Задано подмножество FÎ S, называемое множеством формул исчисления I. Элементы множества F называются формулами.

3. Выделено множество А_ХÎ F формул, называемых аксиомами исчисления I.

4. Имеется конечное множество R отношений R₁R₂…R_n между формулами, называемых правилами вывода, причем если (j₁ j₂ …j_m j) Î R_i, то j называется непосредственно выводимым или непосредственным следствием формул j₁ j₂ …j_m по правилу R_i.

Таким образом, исчислением I будет четверка множеств (А, F, А_Х, R)

А – алфавит исчисления. Буквы алфавита обозначаются символами l₁ l₂…l_n и считается, что начертание букв не влияет на их смысл. Последовательность букв алфавита записанных без пробелов называется словом алфавита и обозначается w = l₁l₂…l_n. Количество букв в слове называется длинной слова.

Выводом формулыj в исчислении I называется конечная последовательность формул j₁ j₂ …j_n такая, что для любого i (1<i<n) формула j_i есть либо аксиома исчисления I, либо непосредственное следствие каких-либо предыдущих формул. (обозначение: )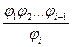

Формула j называется теоремой в исчислении I выводимой в исчислении I (или доказуемой в исчислении I), если существует вывод , который называется выводом формулы j или доказательством теоремы j.

В общем случае может не существовать алгоритма, с помощью которого для произвольной формулы j через конечное число шагов можно определить является ли она выводимой в исчислении I или нет. Если такой алгоритм существует для любой формулы исчисления, то исчисление называется разрешимым. Если в исчислении не все формулы являются доказуемыми, то исчисление называется непротиворечивым.

Используя понятие формального исчисления, определим исчисление высказываний (ИВ).

Алфавит исчисления высказываний состоит из букв А,В,С … А₁,А₂ … В₁,В₂… С… - пропозиционные переменные, логических связок: –, Ù,Ú,® а так же вспомогательных символов (,).

Множество формул ИВ определяется индуктивно:

1) все пропозиционные переменные являются формулами ИВ

2) если j и y - формулы ИВ, то 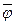, , , - формулы ИВ

3) выражение является формулой ИВ тогда и только тогда, когда это может быть установлено с помощью пунктов 1) и 2).

Дата добавления: 2017-02-01