Алгоритм редукции

Алгоритм Квайна

Алгоритм Квайна позволяет проходить не всё семантическое дерево, а только его часть. Алгоритм состоит в том, что пропозиционным переменным 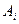, упорядоченным в набор (А₁А₂ … А_к) последовательно приписываются значения 0 и 1, а затем анализируются таблицы истинности формул, содержащих меньшее число переменных.

Пример: проверить общезначимость формулу φ = (((АÙВ)®С)Ù(А®В))®(А®С).

1. упорядочим пропозиционные переменные: (А,В,С)
2. Пусть первая переменныя А принимает значение 1, тогда формула φ преобразуется следующим образом φ = (((1ÙВ)®С)Ù(1®В))®(1®С)«((В®С)ÙВ)®С.
3. а) в полученной формуле предположим, что В принимает значение 1, тогда формула преобразуется следующим образом ((1®С)Ù1)®С«С®С – тождественно истинная формула.

б) предположим, что В принимает значение 0, тогда формула преобразуется следующим образом ((0®С)Ù0)®С«0®С – тождественно истинная формула.

1. пусть переменная А принимает значение 0, тогда формула φ преобразуется следующим образом φ = ((0ÙВ)®СÙ(0®В))®(0®С). При любых значениях В и С получим, φ = 1Ù1®1 = 1 – общезначимое выражение.

Следовательно формула φ является общезначимой.

Алгоритм редукции решает туже задачу, что и алгоритм Квайна – проверка общезначимости формулы, но используется в том случая, когда в формуле содержится большое количество импликаций.

Идея алгоритма состоит в попытке нахождения значений пропозиционных переменных формулы j, при которых значения соответствующей ей функции равно 0. Это возможно сделать на основании того, что импликация является ложной только в том случае, когда посылка истинна, а заключение ложно.

Пример: проверить общезначимость формулы j = ((АÙВ)®С)®(А®(В®С)).

Предположим, что формула j ложна при некотором наборе значений переменных А,В, и С. Тогда булева функция f по этим значениям переменных дает следующие значения формул:

f ((АÙВ)®С) = 1 (*)и f (А®(В®С)) = 0.

Тогда из второй формулы f (А®(В®С)) = 0 следует, что f (А) = 1 и f (В®С) = 0.

Значит f (В) = 1 и f (С) = 0.

Получили, что f (А) = 1, f (В) = 1, f (С) = 0, но при этих значениях справедливо равенство

f ((АÙВ)®С) = 0, что противоречит первой формуле (*). Получили противоречие, значит наше исходное предположение, о том, что при некотором наборе значений переменных А,В, и С j - ложна не верно, значит для любого набора значений переменных А,В, и С j - истина, что равносильно тождественной истинности или общезначимости формулы.

Предикатом называется повествовательное предложение об элементах некоторого предметного множества М, которое становится высказыванием, если все предметные переменные в нем заменить фиксированными элементы из М.

Предикат от k переменных будем называть k – местным предикатом.

Обозначение А(x₁,x₂, … x_k) = А^(k). Высказывание так же считается предикатом – нуль местным предикатом.

Предикат называется разрешимым, если существуют такие наборы конкретных элементов из М, которые обращают предикат в истинное высказывание.

Если предикат при подстановке любых конкретных элементов из множества М обращается в истинное высказывание, то он называется тождественно истинным.

Если предикат при подстановке любых конкретных элементов из множества М обращается в ложное высказывание, то он называется тождественно ложным.

Дата добавления: 2017-02-01