Алгоритм приведения формулы к СКНФ

Алгоритм приведения формулы к СДНФ

1. Привести формулу к ДНФ.

2. Если в конъюнктор входит переменная и ее отрицание, то удаляют этот конъюнктор из формулы.

3. Если в конъюнктор одна и та же переменная (или ее отрицание) входит несколько раз, то удаляют все такие переменные, кроме одной.

4. Если в некоторый конъюнктор не входит переменная y, то заменяют этот конъюнктор на эквивалентный конъюнктор вида , и применяя закон дистрибутивности приводят формулу к ДНФ.

5. Если в полученной ДНФ имеется несколько одинаковых конституент единицы, то оставляют только одну из них. В результате получается СДНФ формулы.

Совершенной конъюнктивной нормальной формой(СКНФ) формулы называется ее КНФ, обладающая следующими свойствами:

1. КНФ не содержит двух одинаковых дизъюнкторов.

2. Ни один из дизъюнкторов не содержит одновременно двух одинаковых переменных.

3. Ни один из дизъюнкторов не содержит одновременно некоторую переменную и ее отрицание.

4. Каждый дизъюнктор содержит либо переменную, либо ее отрицание для всех переменных входящих в формулу.

1. Привести формулу к КНФ.

2. Если в дизъюнктор входит переменная и ее отрицание, то удаляют этот дизъюнктор из формулы.

3. Если в дизъюнктор одна и та же переменная (или ее отрицание) входит несколько раз, то удаляют все такие переменные, кроме одной.

4. Если в некоторый дизъюнктор не входит переменная y, то заменяют этот дизъюнктор на эквивалентный дизъюнктор вида , и применяя закон дистрибутивности приводят формулу к КНФ.

5. Если в полученной КНФ имеется несколько одинаковых конституент нуля, то оставляют только одну из них. В результате получается СКНФ формулы.

Рассмотрим обратную задачу.

Пусть некоторая булева функция f(х₁х₂…х_n) задана своей таблицей истинности. Необходимо по известной таблице истинности построить формулу, представляющую данную функцию. Данная задача не является однозначной, так как существует множество равносильных между собой формул, соответствующих одной функции. На практике чаще всего находят СДНФ или СКНФ формулы. Для этого пользуются следующими свойствами:

1. СДНФ всегда содержит столько конъюнкторов сколько единиц содержится в таблице истинности функции.

2. Переменным, входящим в конъюнктор без знака отрицания соответствует значение переменной 1, а со знаком отрицания - значение переменной 0.

3. СКНФ всегда содержит столько дизъюнкторов сколько нулей содержится в таблице истинности функции.

4. Переменным, входящим в дизъюнктор без знака отрицания соответствует значение переменной 0, а со знаком отрицания - значение переменной 1.

Утверждение: Любую булеву функцию можно представить в виде многочлена от своих переменных.

Многочлен (полином) Жегалкина – это многочлен, являющейся суммой констант нуля или констант единицы и различных одночленов, все переменные в которые входят в степени не выше первой.

Теорема (Жегалкина)

Любая функция единственным образом представима в виде полинома Жегалкина: , суммирование ведется по всем возможным наборам нулей и единиц.

ВАРИАНТ № 1

Задача 1

Используя основные эквивалентности формул, докажите следующие равносильности:

1)

2)

Задача 2

Приведите к ДНФ и КНФ следующие формулы:

1)

2)

Задача 3

Приведите к СДНФ и СКНФ следующие формулы:

1)

2)

Задача 4

Формула задана своей таблицей истинности. Постройте СДНФ и СКНФ этой формулы если:

х	у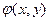

1)

2)

x	y	z

Задача 5

Представьте в виде полинома Жегалкина следующие булевы функции:

1)

2)

ВАРИАНТ № 2

Задача 1

Используя основные эквивалентности формул, докажите следующие равносильности:

1)

2)

Задача 2

Приведите к ДНФ и КНФ следующие формулы:

1)

2)

Задача 3

Приведите к СДНФ и СКНФ следующие формулы:

1)

2)

Задача 4

Формула задана своей таблицей истинности. Постройте СДНФ и СКНФ этой формулы если:

х	у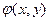

1)

2)

x	y	z

Задача 5

Представьте в виде полинома Жегалкина следующие булевы функции:

1)

2)

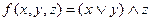
ВАРИАНТ № 3

Задача 1

Используя основные эквивалентности формул, докажите следующие равносильности:

1)

2)

Задача 2

Приведите к ДНФ и КНФ следующие формулы:

1)

2)

Задача 3

Приведите к СДНФ и СКНФ следующие формулы:

1)

2)

Задача 4

Формула задана своей таблицей истинности. Постройте СДНФ и СКНФ этой формулы если:

х	у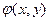

1)

2)

x	y	z

Задача 5

Представьте в виде полинома Жегалкина следующие булевы функции:

1)

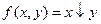
2)

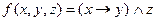
ВАРИАНТ № 4

Задача 1

Используя основные эквивалентности формул, докажите следующие равносильности:

1)

2)

Задача 2

Приведите к ДНФ и КНФ следующие формулы:

1)

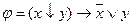
2)

Задача 3

Приведите к СДНФ и СКНФ следующие формулы:

1)

2)

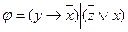
Задача 4

Формула задана своей таблицей истинности. Постройте СДНФ и СКНФ этой формулы если:

х	у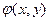

1)

2)

x	y	z

Задача 5

Представьте в виде полинома Жегалкина следующие булевы функции:

1)

2)

ВАРИАНТ № 5

Задача 1

Используя основные эквивалентности формул, докажите следующие равносильности:

1)

2)

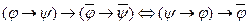
Задача 2

Приведите к ДНФ и КНФ следующие формулы:

1)

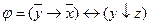
2)

Задача 3

Приведите к СДНФ и СКНФ следующие формулы:

1)

2)

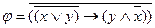
Задача 4

Формула задана своей таблицей истинности. Постройте СДНФ и СКНФ этой формулы если:

х	у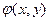

1)

2)

x	y	z

Задача 5

Представьте в виде полинома Жегалкина следующие булевы функции:

1)

2)

Дата добавления: 2017-02-01