Основные эквивалентности формул алгебры логики

1) ассоциативностьÚ и Ù: (j Ùy) Ù c ~ j Ù(y Ù c) (j Úy) Ú c ~ j Ú(y Ú c)

2) коммутативность Ú и Ù: j Ù y ~ y Ù j j Ú y ~ y Ú j

3) идемпотентностьÚ и Ù: y Ù y ~ y y Ú y ~ y

4) дистрибутивность: j Ù(y Ú c) ~ (j Ù y) Ú (j Ù c) j Ú(y Ù c) ~ (j Ú y) Ù (j Ú c)

5) поглощение: j Ù (j Ú y) ~ j j Ú (j Ù y) ~ j

6) Законы Де Моргана: ~ ~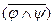

7) двойное отрицание: ~j

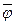8) j ® y ~ Ú y

Формула 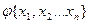называется выполнимой (опровержимой) если существует такой набор переменных, при котором формула принимает значение 1 (значение 0).

Если х – логическая переменная, dÎ{0,1}, то выражение называется литерой.

Литеры х и называются контрарными литерами.

Элементарной конъюнкцией или конъюнктором называется конъюнкция литер.

Элементарной дизъюнкцией или дизъюнктором называется дизъюнкция литер.

Пример: 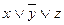-дизъюнктор

- конъюнктор

- одновременно конъюнктор и дизъюнктор

Дизъюнктивной нормальной формой (ДНФ) – называется дизъюнкция конъюнкторов.

Конъюнктивной нормальной формой (КНФ) – называется конъюнкция дизъюнкторов.

Теорема:

1. Для любой формулы существует эквивалентная ей дизъюнктивная нормальная форма.
2. Для любой формулы существует эквивалентная ей конъюнктивная нормальная форма.

Одночлен называется совершенным, если каждая входящая в него переменная входит в него точно один раз со знаком отрицания или без него.

Нормальная форма от некоторых переменных называется совершенной нормальной формой, если каждый входящий в нее одночлен является совершенным одночленом от тех же переменных.

Пусть имеем некоторый набор логических переменных (х₁х₂…х_n) и набор нулей и единиц D=(d₁d₂…d_n).

Конституентой единицы набора D называется конъюнктор вида:

Конституентой нуля набора D называется дизъюнктор вида: .

Заметим, что и тогда и только тогда, когда , , … .

Совершенной ДНФ называется дизъюнкция некоторых конституент единицы, среди которых нет одинаковых. Совершенной КНФ называется конъюнкция некоторых конституент нуля, среди которых нет одинаковых

Конструктивно СДНФ и СКНФ для каждой формулы алгебры высказываний, приведенной к ДНФ или КНФ можно определить следующими свойствами.

Совершенной дизъюнктивной нормальной формой(СДНФ) формулы называется ее ДНФ, обладающая следующими свойствами:

1. ДНФ не содержит двух одинаковых конъюнкторов.

2. Ни один из конъюнкторов не содержит одновременно двух одинаковых переменных.

3. Ни один из конъюнкторов не содержит одновременно некоторую переменную и ее отрицание.

4. Каждый конъюнктор содержит либо переменную, либо ее отрицание для всех переменных входящих в формулу.

Дата добавления: 2017-02-01