
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Учебно-методическое обеспечение
|
|
|
|
КОНТРОЛЬНЫЕ ВОПРОСЫ
Задания к выполнению работы
Пример 1.8
Пример 1.7
Пример 1.6
Пример.1.5
Пример 1.4
Пример 1.3
Пример 1.2
Применим операцию отрицания к высказыванию  : «Нева впадает в Финский залив». Отрицание этого высказывания можно читать так: «Неверно, что
: «Нева впадает в Финский залив». Отрицание этого высказывания можно читать так: «Неверно, что  », то есть «Неверно, что Нева впадает в Финский залив». Перенесем в соответствии с правилами русской грамматики частицу «не» в такое место предложения, чтобы оно звучало именно по-русски, обычно для этого «не» ставят перед сказуемым. Тогда отрицание высказывания
», то есть «Неверно, что Нева впадает в Финский залив». Перенесем в соответствии с правилами русской грамматики частицу «не» в такое место предложения, чтобы оно звучало именно по-русски, обычно для этого «не» ставят перед сказуемым. Тогда отрицание высказывания  примет следующий вид: «Нева не впадает в Финский залив».
примет следующий вид: «Нева не впадает в Финский залив».
Таблица 1.1 дает для данного высказывания следующее логическое значение:  или
или 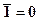 , то есть высказывание
, то есть высказывание  ложно. Ложность высказывания
ложно. Ложность высказывания  обусловлена только истинностью исходного высказывания
обусловлена только истинностью исходного высказывания  и определением, которое мы дали для отрицания высказывания, но никак не самим содержанием, смыслом высказывания
и определением, которое мы дали для отрицания высказывания, но никак не самим содержанием, смыслом высказывания  .
.
Пусть  – высказывание. Так как
– высказывание. Так как  также является высказыванием, то можно образовать отрицание высказывания
также является высказыванием, то можно образовать отрицание высказывания  , то есть высказывание
, то есть высказывание  , которое называется двойным отрицанием высказывания
, которое называется двойным отрицанием высказывания  и читается как «неверно, что не
и читается как «неверно, что не  ». Очевидно, что логические значения высказываний
». Очевидно, что логические значения высказываний  и
и  совпадают
совпадают  .
.
Пусть имеем высказывание  : «Река Нева вытекает из озера Ладога». Отрицанием
: «Река Нева вытекает из озера Ладога». Отрицанием  будет высказывание «Неверно, что река Нева вытекает из озера Ладога» или «Река Нева не вытекает из озера Ладога». А двойным отрицанием
будет высказывание «Неверно, что река Нева вытекает из озера Ладога» или «Река Нева не вытекает из озера Ладога». А двойным отрицанием  будет высказывание «Неверно, что река Нева не вытекает из озера Ладога», то есть исходное высказывание «Река Нева вытекает из озера Ладога».
будет высказывание «Неверно, что река Нева не вытекает из озера Ладога», то есть исходное высказывание «Река Нева вытекает из озера Ладога».
2. Конъюнкция двух высказываний (логическое умножение). Терминпроисходит от лат. conjunctio - соединение.
Конъюнкцией двух высказываний  ,
,  называется новое высказывание, которое считается истинным, если оба высказывания
называется новое высказывание, которое считается истинным, если оба высказывания  ,
,  истинны, и ложным, если хотя бы одно из них ложно.
истинны, и ложным, если хотя бы одно из них ложно.
Конъюнкция высказываний  ,
,  обозначается символом «&» или «
обозначается символом «&» или « »и читается «
»и читается « и
и  ». Высказывания
». Высказывания  ,
,  называются членами конъюнкции.
называются членами конъюнкции.
Логические значения конъюнкции описываются таблицей истинности операции конъюнкции (табл. 1.2).
Таблица 1.2
Таблица истинности операции конъюнкции

| 
| 
|
Применим операцию конъюнкции к высказываниям  : «Саратов находится на берегу Невы» и
: «Саратов находится на берегу Невы» и  : «Все люди смертны». Тогда получим высказывание
: «Все люди смертны». Тогда получим высказывание  : «Саратов находится на берегу Невы и все люди смертны». Естественно, мы не воспримем это высказывание как истинное из-за первой, ложной, его части. К такому же выводу придем, исходя из логических значений исходных высказываний
: «Саратов находится на берегу Невы и все люди смертны». Естественно, мы не воспримем это высказывание как истинное из-за первой, ложной, его части. К такому же выводу придем, исходя из логических значений исходных высказываний  ,
,  , определения конъюнкции и на основании приведенной таблицы истинности (табл. 1.2). Действительно,
, определения конъюнкции и на основании приведенной таблицы истинности (табл. 1.2). Действительно,  =
=  .
.
Из определения операции конъюнкции и отрицания ясно, что высказывание  всегда ложно.
всегда ложно.
Пусть имеем простое высказывание  : «Москва – столица России», тогда
: «Москва – столица России», тогда  : «Москва не столица России». Конъюнкция будет читаться так: «Москва – столица России, и Москва не столица России», что очевидно абсурдно. В соответствии с логическими значениями будем иметь:
: «Москва не столица России». Конъюнкция будет читаться так: «Москва – столица России, и Москва не столица России», что очевидно абсурдно. В соответствии с логическими значениями будем иметь:  или, переставив высказывания местами, получим тот же самый результат
или, переставив высказывания местами, получим тот же самый результат  .
.
3. Дизъюнкция двух высказываний (логическое сложение). Терминпроисходит от лат. dusjunctio - разъединение.
Дизъюнкцией двух высказываний  ,
,  называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний
называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний  ,
,  истинно, и ложным, если они оба ложны.
истинно, и ложным, если они оба ложны.
Дизъюнкция высказываний  ,
,  обозначается символом «
обозначается символом « » и читается «
» и читается « или
или  ». Высказывания
». Высказывания  ,
,  называются членами дизъюнкциии.
называются членами дизъюнкциии.
Логические значения дизъюнкции  связаны с логическими значениями высказываний
связаны с логическими значениями высказываний  ,
,  , как указано в таблице истинности операции дизъюнкции.
, как указано в таблице истинности операции дизъюнкции.
Таблица 1.3
Таблица истинности операции дизъюнкции

| 
| 
|
Пусть имеется высказывание « или
или  »: «В треугольнике
»: «В треугольнике  угол
угол  или
или 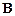 острый». Это высказывание истинно, так как обязательно истинно хотя бы одно из высказываний
острый». Это высказывание истинно, так как обязательно истинно хотя бы одно из высказываний  : «В треугольнике
: «В треугольнике  угол
угол  острый»,
острый»,  : «В треугольнике
: «В треугольнике  угол
угол 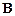 острый».
острый».
К такому же выводу придем, исходя из логических значений исходных высказываний  ,
,  , определения дизъюнкции и на основании приведенной таблицы истинности (см. табл. 1.3). Действительно,
, определения дизъюнкции и на основании приведенной таблицы истинности (см. табл. 1.3). Действительно,  =
=  .
.
В повседневной жизни союз «или» употребляется в различном смысле: исключающем и неисключающем. Так, если в приведенном высказывании о треугольнике союз «или» используется в не исключающем смысле, так как оба высказывания не отрицают друг друга, то в высказывании «Или ты сейчас играешь на компъютере, или ты завтра не пойдешь играть в футбол» союз «или» используется в исключающем смысле, так как одно высказывание «Или ты сейчас играешь на компъютере» исключает другое «И ли ты завтра не пойдешь играть в футбол».
Из определения операции дизъюнкции и отрицания ясно, что высказывание  всегда истинно, то есть
всегда истинно, то есть  .
.
4. Импликация двух высказываний. Терминпроисходит от лат. implication – сплетение и implico – тесно связываю.
Импликацией двух высказываний  ,
,  называется новое высказывание, которое считается ложным, если
называется новое высказывание, которое считается ложным, если  истинно, а
истинно, а  - ложно, и истинным во всех остальных случаях.
- ложно, и истинным во всех остальных случаях.
Импликация высказываний  ,
,  обозначается символом «
обозначается символом « » и читается: «если
» и читается: «если  , то
, то  », или «из
», или «из  следует
следует  » ", или «
» ", или « влечет
влечет  », или «
», или « достаточно для
достаточно для  » и т.д. Высказывания
» и т.д. Высказывания  ,
,  называются членами импликации. Высказывание
называются членами импликации. Высказывание  называется условием, посылкой или антецедентом, высказывание
называется условием, посылкой или антецедентом, высказывание  - следствием, заключением или консеквентом, высказывание
- следствием, заключением или консеквентом, высказывание 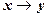 - следованием или импликацией.
- следованием или импликацией.
Логические значения импликации 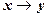 связаны с логическими значениями высказываний
связаны с логическими значениями высказываний  ,
,  , как указано в таблице истинности операции импликации (табл. 1.4).
, как указано в таблице истинности операции импликации (табл. 1.4).
Таблица 1.4
Таблица истинности операции импликации

| 
| 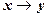
|
5. Эквивалентность (эквиваленция) двух высказываний. Эквивалентностью двух высказываний  ,
,  называется новое высказывание, которое считается истинным, когда оба высказывания
называется новое высказывание, которое считается истинным, когда оба высказывания  ,
,  либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.
либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.
Эквивалентность высказываний  ,
,  обозначается символом «
обозначается символом «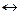 » и читается: «для того, чтобы
» и читается: «для того, чтобы  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы  » или «
» или « тогда и только тогда, когда
тогда и только тогда, когда  », или «
», или « эквивалентно
эквивалентно  », или «
», или «  , если и только если
, если и только если  ». Высказывания
». Высказывания  ,
,  называются членами эквивалентности (эквиваленции).
называются членами эквивалентности (эквиваленции).
Логические значения эквивалентности  связаны с логическими значениями высказываний
связаны с логическими значениями высказываний  ,
,  , как указано в таблице истинности операции эквивалентности.
, как указано в таблице истинности операции эквивалентности.
Таблица 1.5
Таблица истинности операции эквивалентности

| 
| 
|
Сложное высказывание – эквивалентность  «Треугольник
«Треугольник  с вершиной В и основанием АС равнобедренный тогда и только тогда, когда
с вершиной В и основанием АС равнобедренный тогда и только тогда, когда  » является истиной, так как простые высказывания «Треугольник
» является истиной, так как простые высказывания «Треугольник  с вершиной В и основанием АС равнобедренный» и «В треугольнике
с вершиной В и основанием АС равнобедренный» и «В треугольнике  с вершиной В и основанием АС
с вершиной В и основанием АС  » либо одновременно истинны, либо одновременно ложны.
» либо одновременно истинны, либо одновременно ложны.
Действительно, исходя из логических значений и используя таблицу истинности эквивалентности (см. табл. 1.5), получим  .
.
Высказывание  «13 < 5 тогда и только тогда, когда снег белый», являющееся эквивалентностью высказываний
«13 < 5 тогда и только тогда, когда снег белый», являющееся эквивалентностью высказываний  «13 < 5» и
«13 < 5» и  «снег белый» ложно, так как ложно первое высказывание и истинно второе. Логические значения также свидетельствуют об этом
«снег белый» ложно, так как ложно первое высказывание и истинно второе. Логические значения также свидетельствуют об этом  .
.
Эквивалентность имеет большое значение в математических доказательствах. Значительное число теорем формулируется в форме необходимых и достаточных условий, то есть в форме эквивалентности. Тогда, зная об истинности или ложности одного из двух членов эквивалентности и доказав истинность самой эквивалентности, мы заключаем об истинности или ложности второго члена эквивалентности.
 1. Пусть a -высказывание «Студент Иванов изучает английский язык», b - высказывание «Студент Иванов успевает по математической логике». Дать словесную формулировку высказываний.
1. Пусть a -высказывание «Студент Иванов изучает английский язык», b - высказывание «Студент Иванов успевает по математической логике». Дать словесную формулировку высказываний.
 1)
1)  2)
2)  3)
3)  4)
4)  ; 5)
; 5)  .
.
Решение примера 1.
«Студент Иванов изучает английский язык и не успевает по математической логике».
2. Определить, какие из следующих предложений являются высказываниями, и установить, если это возможно, истинны они или ложны:
1) Москва – столица России;
2) Студент физико-математического факультета;
3)  ;
;
4) Луна есть спутник Марса;
5) Сумма углов в треугольнике равна 180°;
6)  ;
;
7) На улице идет дождь.
Решение примера 1.
Согласно определению высказывание – это утвердительное повествовательное предложение, которое для данных условий места и времени является либо истинным, либо ложным. Из определения следует, что первое предложение отвечает данному определению, следовательно, оно является высказыванием. Поскольку Москва действительно является столицей России, то данное высказывание истинно.
3. Среди следующих высказываний указать элементарные и составные. В составных высказываниях выделить грамматические связки:
1) число 27 не делится на 3;
2) число 15 делится на 5 и на 3;
3) если число 126 делится на 9, то оно делится на 3;
4) число 7 является делителем числа 42;
5) число 1269 делится на 9 тогда и только тогда, когда 18 делится на 9.
Решение примера 1.
Согласно определению, высказывание, представляющее собой одно утверждение, называется простым или элементарным.
Другое определение - высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если…, то…», «тогда и только тогда», называются сложными или составными.
Согласно данным определениям, первое высказывание состоит из одного простого утверждения: «число 27 делится на 3», и грамматической связки «не», с помощью которой образуется новое высказывание «число 27 не делится на 3», которое, следовательно, становится составным.
4. Пусть p и q обозначают высказывания;
p - «Я учусь в школе», q – «Я люблю математику».
Прочитайте следующие сложные высказывания:
1)  2)
2)  3)
3)  4)
4)  5)
5)  6)
6)  7)
7)  8)
8)  .
.
Решение примера 1.
«Я не учусь в школе».
5. Какие из следующих импликаций истинны?
1) Если  ; 2) Если
; 2) Если  ;
;
3) Если  ; 4)Если
; 4)Если  .
.
Решение примера 1.
Согласно определению, и м ликацией двух высказываний  ,
,  называется новое высказывание, которое считается ложным, если
называется новое высказывание, которое считается ложным, если  истинно, а
истинно, а  - ложно, и истинным во всех остальных случаях.
- ложно, и истинным во всех остальных случаях.
В данном примере высказыванием х является выражение  , которое является истинным, а высказыванием у – выражение
, которое является истинным, а высказыванием у – выражение  , которое также является истинным, следовательно, импликация, представленная выражением (1) согласно определению является истинным.
, которое также является истинным, следовательно, импликация, представленная выражением (1) согласно определению является истинным.
6. Выясните, в каких случаях приведенные ниже данные противоречивы:
1) 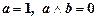 ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  .
.
Решение примера 1.
Данный пример имеет операцию конъюнкции. Согласно ее определению конъюнкциейдвух высказываний  ,
,  называется новое высказывание, которое считается истинным, если оба высказывания
называется новое высказывание, которое считается истинным, если оба высказывания  ,
,  истинны, и ложным, если хотя бы одно из них ложно. В высказывании имеются две переменные а и b, одна из них, а задана и равна 1, другая b не задана и поэтому может принимать любое значение: или 1, или 0. Поскольку при значении b = 1 выражение
истинны, и ложным, если хотя бы одно из них ложно. В высказывании имеются две переменные а и b, одна из них, а задана и равна 1, другая b не задана и поэтому может принимать любое значение: или 1, или 0. Поскольку при значении b = 1 выражение  становится неверным, то данные являются противоречивыми.
становится неверным, то данные являются противоречивыми.
7. Проверить, не составляя таблиц истинности, являются ли следующие формулы тождественно истинными.
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 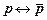 ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10)  ;
;
11)  ; 12)
; 12)  :
:
13)  ; 14)
; 14)  .
.
Решение примера 1.
Тождественно истинная формула – формула, которая принимает значение 1 при всех значениях входящих в нее переменных.
Данный пример имеет операцию импликации. Импликацией двух высказываний  ,
,  называется новое высказывание, которое считается ложным, если
называется новое высказывание, которое считается ложным, если  истинно, а
истинно, а  - ложно, и истинным во всех остальных случаях. В примере и условие
- ложно, и истинным во всех остальных случаях. В примере и условие  , и следствие
, и следствие  равны
равны  , следовательно, согласно определению операции импликации формула является тождественно истинной, поскольку ложной она является только когда условие
, следовательно, согласно определению операции импликации формула является тождественно истинной, поскольку ложной она является только когда условие  истинное, а следствие
истинное, а следствие  ложное, то есть когда они имеют разное значение. В нашем примере они всегда одинаковы, следовательно, при любых значениях
ложное, то есть когда они имеют разное значение. В нашем примере они всегда одинаковы, следовательно, при любых значениях  формула принимает значение 1 и является тождественно истинной.
формула принимает значение 1 и является тождественно истинной.
8. Найдите логические значения  и
и  , при которых выполняются равенства:
, при которых выполняются равенства:
1) 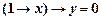 ; 2)
; 2)  ; 3)
; 3)  .
.
Решение примера 1.
Импликация данного примера равна 0, если условие  равно 1, а следствие
равно 1, а следствие  . Условие
. Условие  , представляющее собой импликацию равно 1, только если
, представляющее собой импликацию равно 1, только если  . Отсюда значение
. Отсюда значение  , а
, а  .
.
9. Определить значения следующих выражений при заданных условиях.
1)Известно, что импликация  истинна, а эквивалентность
истинна, а эквивалентность  ложна. Что можно сказать о значении импликации
ложна. Что можно сказать о значении импликации  ?
?
2) Известно, что эквивалентность  истинна. Что можно сказать о значении
истинна. Что можно сказать о значении
 и
и 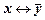 ?
?
 3) Известно, что
3) Известно, что  имеет значение 1. Что можно сказать о значениях импликации
имеет значение 1. Что можно сказать о значениях импликации  ;
;  ?
?
4) Известно, что 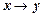 имеет значение 1. Что можно сказать о значениях
имеет значение 1. Что можно сказать о значениях
 ;
;  ;
;  ?
?
Решение примера 1.
Рассмотрим эквивалентность  , которая ложна. Согласно определению эквивалентность ложна, если члены эквивалентности имеют разные значения, то есть значение
, которая ложна. Согласно определению эквивалентность ложна, если члены эквивалентности имеют разные значения, то есть значение  не равно значению
не равно значению  . Далее используем то условие, что импликация
. Далее используем то условие, что импликация 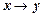 истинна. Согласно определению импликации при разных значениях
истинна. Согласно определению импликации при разных значениях  и
и  она может быть истинной только, если условие
она может быть истинной только, если условие  ложно, а
ложно, а  истинно. Отсюда следует, что импликация
истинно. Отсюда следует, что импликация  ложна.
ложна.
10. Пусть  ,
,  ,
,  . Определить логические значения нижеследующих сложных высказываний:
. Определить логические значения нижеследующих сложных высказываний:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  .
.
Решение примера 1.
 .
.

 11. Показать, что логические связки
11. Показать, что логические связки  ,
,  ,
,  ,
, 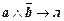 , где л - фиксированное ложное высказывание, имеют ту же таблицу истинности, что и импликация
, где л - фиксированное ложное высказывание, имеют ту же таблицу истинности, что и импликация  .
.
12. Составить таблицы истинности для формул:
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
Решение примера 7.
В таблице истинности должны быть все комбинации нулей и единиц всех независимых переменных. Поскольку число независимых переменных равно  , которое в числовом выражении может быть любым, то необходимо найти закономерности, при которых функция сохраняет свое значения и приводить те значения переменных (строк), на которых функция меняет свое значение.
, которое в числовом выражении может быть любым, то необходимо найти закономерности, при которых функция сохраняет свое значения и приводить те значения переменных (строк), на которых функция меняет свое значение.
Таблица 1.6
Таблица истинности к примеру 7

| 
| … | 
| 
| 
|
| … | |||||
| … | |||||
| … | |||||
| … | … | … | … | … | … |
| … | |||||
| … | |||||
| … | … | … | … | … | … |
| … |
13. Исключающей дизъюнкцией двух высказываний  и
и  называется новое высказывание, обозначаемое
называется новое высказывание, обозначаемое 
 (читают «либо
(читают «либо  , либо
, либо  »), которое истинно, когда одно и только одно из данных высказываний истинно, и ложно в остальных случаях. Составить таблицу истинности исключающей дизъюнкции и выразить ее через основные операции над высказываниями.
»), которое истинно, когда одно и только одно из данных высказываний истинно, и ложно в остальных случаях. Составить таблицу истинности исключающей дизъюнкции и выразить ее через основные операции над высказываниями.
1. Что изучает алгебра высказываний?
2. Дать определение высказывания. Охарактеризуйте простое и составное высказывание.
3. Определение отрицания высказывания. Таблица истинности.
4. Определение операции конъюнкции. Таблица истинности.
5. Определение операции дизъюнкции. Таблица истинности.
6. Определение операции импликации. Таблица истинности.
7. Определение операции эквиваленции. Таблица истинности.
8. В выражении  высказывания
высказывания  ,
,  ,
,  заданы, причем
заданы, причем  и
и  истинны, а
истинны, а  ложно. Истинно или ложно высказывание
ложно. Истинно или ложно высказывание  ? Как выражается
? Как выражается  через
через  ,
,  ,
,  ?
?
1. Лихтарников, Л. М. Математическая логика: курс лекций / Л. М. Лихтарников, Т. Г. Сукачева. – СПб.: Лань, 1998.
2. Игошин, В. И. Математическая логика и теория алгоритмов / В. И. Игошин. – М.: ACADEMA, 2004.
3. Шапорев, С. Д. Математическая логика: курс лекций и практических занятий / С. Д. Шапорев – СПб.: БХВ – Петербург, 2005.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 121; Нарушение авторских прав?; Мы поможем в написании вашей работы!