Функции алгебры логики

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ. СОВЕРШЕННЫЕ НОРМАЛЬНЫЕ ФОРМЫ

Лабораторная работа № 3

ЦЕЛЬ РАБОТЫ – изучение функций алгебры логики и способов получения совершенных нормальных форм.

Значение формул алгебры логики полностью зависит от значений входящих в эту формулу высказываний. Поэтому формула алгебры логики является функцией входящих в нее элементарных высказываний.

Например, формула является функцией трех переменных . Особенностью этой функции является то обстоятельство, что ее аргументы принимают одно из двух значений: ноль или единицу, и при этом функция также принимает одно из двух значений: ноль или единицу.

Функция алгебры логики переменных (или функция Буля) – функция переменных 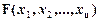, где каждая переменная принимает два значения: 0 и 1, и при этом функция может принимать только одно из двух значений: 0 или 1.

Любая формула алгебры логики является и функцией алгебры логики. Очевидно, что тождественно истинные и тождественно ложные формулы алгебры логики представляют собой постоянные функции, а две равносильные формулы выражают одну и ту же функцию.

Определим, каково количество функций 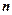переменных. Каждую функцию алгебры логики, как и формулу алгебры логики, можно задать с помощью таблицы истинности, которая будет содержать строк. Следовательно, каждая функция 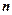переменных принимает значений, состоящих из нулей и единиц. Таким образом, функция 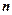переменных полностью определяется набором значений из нулей и единиц длины .

Общее количество наборов, состоящих из нулей и единиц длины , равно 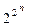. Значит, общее количество различных функций алгебры логики 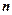переменных равно .

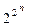В соответствии с данной формулой различных функций одной переменной будет , а различных функций двух переменных – , . Выпишем все функции алгебры логики одной и двух переменных.

Булевы функции от одной переменной.

Булевой функцией от одной переменной называется функция f, заданная на множестве из двух элементов и принимающая значения в том же двухэлементном множестве.

Элементы двухэлементного множества будем обозначать 0 и 1. Тогда .

Составим таблицу истинности для различных функций одной переменной. Она будет иметь вид табл.3.1.

Таблица 3.1

Таблица истинности всех функций одной переменной

Из данных таблицы следует, что две функции одной переменной будут постоянными: и , а две переменными: и .

Таким образом, всего будет иметься четыре различные булевы функции одного аргумента:

– функция, тождественно равная 0 (тождественный нуль);

– тождественная функция;

– функция, называемая отрицанием;

– функция, тождественно равная 1(тождественная единица).

Булевы функции от двух переменных. Булевой функцией от двух переменных называется функция f, заданная на множестве и принимающая значения в двухэлементном множестве .

Составим таблицу истинности для всевозможных функций от двух переменных аналогично порядку составления таблицы истинности от одной переменной (табл. 3.1). При этом в первой строчке приведем сокращенные обозначения всех рассмотренных нами ранее операций, во второй – сокращенные обозначения функций, то есть .

Многие из функций в табл. 3.2 имеют названия и специальные обозначения. Приведем их, сгруппировав функции в пары по тому принципу, что каждая функция из пары является отрицанием другой функции этой пары.

Таблица 3.2

Таблица истинности всех функций двух переменных

|

1. – тождественный ноль,

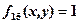– тождественная единица.

2. – конъюнкция,

– отрицание конъюнкции – штрих Шеффера.

3. – дизъюнкция,

– отрицание дизъюнкции – стрелка Пирса (или штрих Лукасевича).

4. – импликация,

– отрицание импликации (специального названия нет).

5. – антиимпликация или обратная импликация, в которой посылка , а следствие ,

– отрицание антиимпликации (без специального названия).

6. 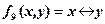- эквивалентность,

– отрицание эквивалентности или сложение по модулю два.

7. – всегда принимает значения, равные переменной ,

– всегда принимает значения, равные отрицанию переменной .

8. – всегда принимает значения, равные переменной ,

– всегда принимает значения, равные отрицанию переменной .

Из введенных простейших булевых функций можно строить с помощью суперпозиций более сложные булевы функции. Например, если в функцию вставить вместо аргумента t функцию , то получим следующую сложную функцию: . Если в нее, в свою очередь, вставить вместо аргумента z функцию , то получим сложную функцию 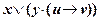. И так далее. В результате можно получить булевы функции от трех, четырех и большего числа переменных.

Дата добавления: 2017-02-01