СДНФ и СКНФ операции конъюнкции

Задания к выполнению работы

Решение

Пример 3.3

Установить класс формулы .

Приводим формулу к какой-либо нормальной форме:

Полученная ДНФ А не является тождественно ложной, так как не каждая элементарная конъюнкция содержит переменную и ее отрицание. Следовательно, исходная формула тождественно истинна или выполнима. Для дальнейшего решения преобразуем ее к КНФ.

Полученная КНФ А не является тождественно истинной, поскольку не каждая элементарная дизъюнкция содержит переменную и ее отрицание.

Таким образом, исходная формула не является ни тождественно ложной, ни тождественно истинной, следовательно, она выполнима.

Проверим это с помощью таблицы истинности

Таблица 3.5

Таблица истинности формулы

В соответствии с определением формула является выполнимой, если она принимает значение 1 хотя бы на одном наборе значений входящих в нее переменных и при этом не является тождественно истинной. По таблице истинности (табл. 3.5) видно, что формула отвечает именно такому определению и, следовательно, является выполнимой.

1. По таблице истинности (табл. 3.5) найдите формулы СДНФ А и СКНФ А, определяющие функции , , , , и придайте им более простой вид.

Таблица 3.5

Таблица истинности для нахождения формул СДНФ А и СКНФ А

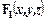
2. Для каждой булевой функции от двух переменных найдите двойственную ей булеву функцию.

3. Булева функция 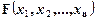называется:

а) сохраняющей 0, если ;

б) сохраняющей 1, если .

Среди булевых функций от одной и от двух переменных найти все функции, сохраняющие 1, и все функции, сохраняющие 0 (функции см. п. 3.1.1).

4. Для следующих формул найти СДНФ А и СКНФ А, каждую двумя способами (путем равносильных преобразований и используя таблицы истинности):

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

5. Докажите равносильность формул и 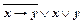сравнением их совершенных нормальных форм (конъюнктивных или дизъюнктивных).

6. Найдите более простой вид формул, имеющих следующие совершенные нормальные формы:

1)

2)

3)

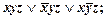
4)

7. Используя только критерий тождественной истинности и тождественной ложности формулы, установить, будет ли данная формула тождественно истинной, тождественно ложной или выполнимой:

1)

2)

3)

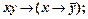
4)

5)

6)

8. Пусть – функция алгебры логики (булева функция), которая принимает значение 1 тогда и только тогда, когда точно две переменные принимают значение 1. Выразите эту функцию через основные логические операции.

9. НайдитеСДНФ А для любой тождественно истинной формулы, содержащей: 1) одну переменную, 2) две переменные, 3) три переменные.

10. НайдитеСКНФ А для любой тождественно ложной формулы, содержащей: 1) одну переменную, 2) две переменные, 3) три переменные.

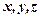11. Построить формулу от переменных так, чтобы

.

12. Доказать равносильности второй группы.

1. .

2. .

законы де Моргана

3.

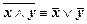
4.

Решение примера 2.

Для решения примера необходимо составить таблицу истинности, получить по ней совершенные формы СДНФ F и СКНФ F, затем преобразовать СДНФ F в СКНФ F или СКНФ F в СДНФ F и объединить в одну из форм СДНФ F или СКНФ F, а после упрощения совершенных форм получить требуемое выражение:

а) составляем таблицу истинности (табл. 3.6);

б) по таблице истинности составляем СДНФ F и СКНФ F:

СДНФ , СКНФ ;

в) преобразуем СКНФ F в СДНФ F (или наоборот СДНФ F вСКНФ F)

СДНФ F = .

Таблица 3.6

Таблица истинности для нахождения формул

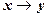
г) объединяем путем суммирования функций в одну – СДНФ:

Равносильность доказана.

Дата добавления: 2017-02-01