Проблема разрешимости

Решение

Пример 3.2

Правило получения СКНФ А с помощью равносильных преобразований.

1. Для формулы А получаем любую КНФ А.

2. Из КНФ А путем равносильных преобразований получаем СКНФ А, последовательно добиваясь выполнения четырех свойств СКНФ – свойств совершенства, которые аналогичны свойствам совершенства СДНФ.

1) Пусть В есть сомножитель (дизъюнкция) КНФ А вида 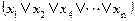, не содержащий (в данном случае ). Для введения ее в сомножитель (дизъюнкцию) используем равносильность . Для этого складываем ее с В и получим дизъюнкцию . Далее применяем закон дистрибутивности дизъюнкции относительно конъюнкции , что позволит заменить исходную дизъюнкцию В на две, которые уже будут содержать недостающую переменную

.

2) Если в КНФ А входят две одинаковых элементарных дизъюнкции В, то лишнюю можно отбросить, пользуясь равносильностью .

3) Если некоторая элементарная дизъюнкция В, входящая в КНФ А, содержит переменную и ее отрицание , то ее можно исключить из КНФ А, как единичный член конъюнкции ввиду равносильности .

4) Если некоторая элементарная дизъюнкция, входящая в КНФ А, содержит переменную дважды, то одну переменную можно отбросить, пользуясь равносильностью .

После выполнения указанных процедур будет получена СКНФ А.

Из формулы А получить СКНФ А с помощью таблицы истинности и с помощью равносильных преобразований.

Для иллюстрации получения СКНФ А используем формулу из предыдущего примера 3.1.

1. Получение СДНФ А с помощью таблицы истинности.

Поскольку формула осталась та же, то останется такой же и таблица истинности этой формулы (табл. 3.3).

1 -й способ. Получение СКНФ А с использованием формулы .

Для этого необходимо сначала получить с помощью таблицы .

Затем следует взять отрицание и использовать закон де Моргана для его снятия:

Таким образом, получена :

2 -й способ. Получение СКНФ А сразу по таблице истинности.

В этом случае для каждого набора значений переменных, на котором функция 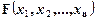принимает значение, равное 0, запишем дизъюнкцию элементарных переменных высказываний, взяв за член конъюнкции , если значение на указанном наборе значений переменных есть 0, и отрицание , если значение есть 1. Конъюнкция всех записанных дизъюнкций и будет искомой формулой. Сразу получим искомую формулу

2. Получение СДНФ А с помощью равносильных преобразований.

1) В соответствии с правилом получения СКНФ из формулы А с помощью равносильных преобразований для формулы А получаем любую КНФ А.

КНФ А = .

Далее для получения СКНФ А применяем закон дистрибутивности дизъюнкции относительно конъюнкции .

В полученной КНФ А, в дизъюнкции, заключенной в скобках, не хватает всего одной переменной , поэтому добавим к ней произведение равное нулю и получим выражение 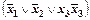. Применяя закон дистрибутивности к этому выражению, в качестве переменной данного закона можно взять исходную дизъюнкцию 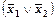, в качестве взять , а в качестве – . Тогда будем иметь два сомножителя, которые войдут в СКНФ А:

.

Осталась еще одна переменная за скобками. Для превращения ее в элементарные дизъюнкции (сомножители СКНФ А) добавим к ней сначала произведение недостающей переменной , применим к полученному выражению закон дистрибутивности, затем к полученным выражениям добавим произведение недостающей переменной и снова применим закон дистрибутивности

Объединяя полученные сомножители с полученными ранее, располагая для удобства анализа переменные в порядке возрастания и приводя подобные члены, получим СКНФ А:

Как видно, полученная с помощью равносильных преобразований СКНФ А, такая же, как и СКНФ А, полученная по таблице истинности.

Все формулы алгебры логики делятся на три класса:

1) тождественно истинные;

2) тождественно ложные;

3) выполнимые.

Определения тождественно истинной и тождественно ложной формул были даны ранее.

Выполнимой формулой А называется формула, которая принимает значение «истина» хотя бы на одном наборе значений входящих в нее переменных и при этом не является тождественно истинной.

В связи с этим возникает задача: к какому классу относится данная формула? Эта задача носит название проблемы разрешимости.

Данная проблема в действительности разрешима, поскольку для каждой формулы алгебры логики может быть записана таблица истинности, которая и даст ответ на поставленный вопрос. Трудность состоит в том, что практическое использование таблицы истинности для формулы при больших проблематично.

Поэтому существует другой способ, позволяющий, не используя таблицы истинности, определить, к какому классу относится формула А. Этот способ основан на приведении формулы к нормальной форме (КНФ или ДНФ) и использовании алгоритма, который позволяет определить, является ли данная формула тождественно истинной или не является. При этом решается вопрос о том, будет ли формула А выполнимой.

Теорема. Для того, чтобы формула алгебры логики А была тождественно истинна (ложна), необходимо и достаточно, чтобы каждая дизъюнкция (конъюнкция), входящая в КНФ А (ДНФ А), содержала переменную и ее отрицание.

Дата добавления: 2017-02-01