Учебно-методическое обеспечение

КОНТРОЛЬНЫЕ ВОПРОСЫ

Задания к выполнению работы

1. Установить, используя равносильные преобразования, какие из следующих формул являются тождественно истинными, тождественно ложными:

1)

2)

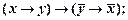
3)

4)

5)

6)

7)

8)

9)

10)

Решение примера 1.

Подвергнем формулу 1 равносильным преобразованиям

В результате преобразований получилось, что формула равна 0, следовательно, при всех значениях переменных она равняется нулю и согласно определению тождественно ложной формулы является тождественно ложной.

2. Доказать равносильности:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

Решение примера 1.

Для доказательства равносильности формулы 1 подвергнем ее левую часть равносильным преобразованиям

3. Упростить формулы:

1)

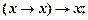
2)

3)

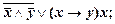
4)

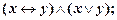
5)

6)

7)

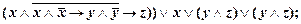
8)

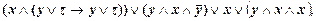
9)

10)

Решение примера 1.

Напомним, что формула А считается проще равносильной ей формулы В, если она содержит меньше переменных и меньше логических операций. Для упрощения используем равносильные преобразования. Для компактности записи будем опускать знак конъюнкции

.

4. Доказать тождественную истинность или тождественную ложность формул:

1)

2)

3)

4)

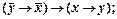
5)

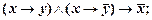
6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

Решение примера 14).

5. Пусть А – тождественно ложная формула. Доказать, что

.

6. Штрихом Лукасевича (стрелкой Пирса) двух высказываний и называется новое высказывание, обозначаемое 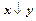(читается «ни , ни », которое истинно в том и только в том случае, когда оба данные высказывания ложны. Составить таблицу истинности штриха Лукасевича и выразить его через основные операции над высказываниями (конъюнкцию, дизъюнкцию и отрицание).

7. Выразить операции импликации, эквиваленции, стрелку Пирса, штрих Шеффера, суммирование по модулю два:

1) через операции конъюнкции и отрицание;

2) через операции дизъюнкции и отрицание;

3) через операции импликации и отрицание.

1. Дать определение формулы высказываний.

2. Какова приоритетность выполнения логических операций?

3. Какие формулы алгебры высказываний являются равносильными?

4. Дать определение тождественно истинной и тождественно ложной формулы.

5. Сколько строк содержит таблица истинности формулы при наличии в ней 6 переменных?

6. Привести основные равносильности.

7. Записать равносильности, выражающие одни логические операции через другие.

8. Привести равносильности, выражающие основные законы алгебры логики.

9. С помощью каких равносильностей можно заменить любую формулу равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание?

10. Какая связь существует между понятиями равносильности и эквивалентности?

11. С помощью какой операции может быть выражена любая из пяти рассмотренных нами в первой работе логических операций? Дать ее определение и привести ее таблицу истинности.

12. Преобразовать формулу к виду, содержащему только одну операцию.

13. Найдите , если .

14. Выразить отрицание импликации через основные операции так, чтобы отрицания стояли только над аргументами.

1. Лихтарников, Л. М. Математическая логика: курс лекций / Л. М. Лихтарников, Т. Г. Сукачева. – СПб.: Лань, 1998

2. Игошин, В. И. Математическая логика и теория алгоритмов / В. И. Игошин. – М.: ACADEMA, 2004.

3. Шапорев, С. Д. Математическая логика: курс лекций и практических занятий / С. Д. Шапорев – СПб.: БХВ – Петербург, 2005.

Дата добавления: 2017-02-01