Равносильные формулы алгебры высказываний

Две формулы алгебры логики А и В называются равносильными, если они принимают одинаковые логические значения на любом одинаковом наборе значений входящих в формулы элементарных высказываний.

Равносильность формул обычно обозначается знаком , а запись означает, что формулы А и В равносильны.

Например, равносильны формулы:

, , .

Формула А называется тождественно истинной (или тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных.

Например, тождественно истинны формулы , .

Формула А называется тождественно ложной, если она принимает значение 0 при всех значениях входящих в нее переменных.

Например, тождественно ложна формула . Отношение равносильности рефлексивно, симметрично и транзитивно.

Между понятиями равносильности и эквивалентности существует следующая связь: если формулы А и В равносильны, то формула - тавтология, и обратно, если формула - тавтология, то формулы А и В равносильны.

Важнейшие равносильности алгебры логики можно разбить на три группы.

I. Основные равносильности:

	законы идемпотентности

1.

2.

3.

4.

5.

6.

7. - закон противоречия.

8. - закон исключения третьего.

9. - закон снятия двойного отрицания.

законы поглощения

10.

11.

II. Равносильности, выражающие одни логические операции через другие:

1. .

2. .

законы де Моргана

3.

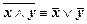
4.

5. .

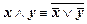6. .

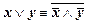Очевидно, что равносильности 5 и 6 получаются из равносильностей 3 и 4 соответственно, если от обеих частей последних взять отрицания и воспользоваться законом снятия двойного отрицания.

Из равносильностей этой группы следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание.

Дальнейшее исключение логических операций невозможно. Так, если использовать только конъюнкцию, то такая формула, как отрицание , не может быть выражена с помощью операции конъюнкции.

Однако существуют операции, с помощью которых может быть выражена любая из пяти рассмотренных нами логических операций.

Такой операцией является, в частности, операция «Штрих Шеффера».

Операцией штрих Шеффера двух высказываний называется новое высказывание, которое считается ложным, когда оба высказывания одновременно истинны, и истинным во всех остальных случаях.

Штрих Шеффера обозначается символом и читается « не совместно с ».

Логические значения штриха Шеффера связаны с логическими значениями высказываний , как указано в таблице истинности операции штрих Шеффера (табл. 2.2).

Таблица 2.2

Таблица истинности операции штрих Шеффера

Очевидно, что в соответствии с данной таблицей истинности имеют место равносильности:

1. .

2. .

Из этих двух равносильностей следует, что всякая формула алгебры логики может быть заменена равносильной формулой, содержащей только операцию штрих Шеффера.

Необходимо отметить, что .

Аналогично может быть введена операция (функция) .

.

III. Равносильности, выражающие основные законы алгебры логики:

1. - коммутативность конъюнкции.

2. - коммутативность дизъюнкции.

3. - ассоциативность конъюнкции.

4. - ассоциативность дизъюнкции.

5. - дистрибутивность конъюнкции относительно дизъюнкции.

6. - дистрибутивность дизъюнкции относительно конъюнкции.

На основе равносильностей I, II и III групп можно часть формулы или всю формулу заменить равносильной ей формулой. Такие преобразования формул называются равносильными.

Равносильные преобразования используются для доказательства равносильностей, для приведения формул к заданному виду, для упрощения формул.

Формула А считается проще равносильной ей формулы В, если она содержит меньше переменных и меньше логических операций. При этом обычно операции эквивалентность и импликация заменяются операциями дизъюнкции и конъюнкции, а отрицание относят к элементарным высказываниям.

Дата добавления: 2017-02-01