Дизъюнктивная нормальная форма (ДНФ) и совершенная дизъюнктивная нормальная форма (СДНФ)

Закон двойственности

Пусть формула А содержит только операции конъюнкции, дизъюнкции и отрицания.

Будем называть операцию конъюнкции двойственной операции дизъюнкции, а операцию дизъюнкции двойственной операции конъюнкции.

Формулы А и А^* называются двойственными, если формула А^* получается из формулы А путем замены в ней каждой операции на двойственную.

Например, для формулы двойственной формулой будет формула .

Если формулы А и В равносильны, то равносильны и им двойственные формулы, то есть .

Если для формулы двойственной формулой является , то справедлива равносильность

.

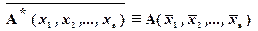Если взять отрицание от левой и правой части данного равенства, то получится выражение

.

Применяя данное выражение для определения двойственной к выражению формулы, получим

.

Формула полностью совпала с ранее полученным в соответствии с определением двойственных формул выражением.

Самодвойственная формула – формула равносильная своей двойственной формуле. Такая формула отвечает условию

.

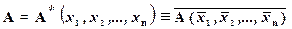Самодвойственная функция принимает на противоположных наборах и 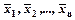противоположные значения.

Элементарной конъюнкцией 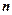переменных называется конъюнкция переменных или их отрицаний.

Элементарная конъюнкция 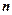переменных может быть записана в виде:

или , или , или

и т. д.

Дизъюнктивной нормальной формой формулы А называется равносильная ей формула, представляющая собой дизъюнкцию конъюнкций.

Дизъюнкция элементарных конъюнкций 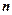переменных формулы А может быть записана в виде:

Совершенной дизъюнктивной нормальной формой формулы А называется равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций.

Среди большого числа ДНФ А, как уже говорилось, существует единственная ДНФ А, для которой выполняются перечисленные выше четыре свойства совершенства, свойства (С). На этом основании можно дать следующее определение такой ДНФ.

Совершенная дизъюнктивная нормальная форма формулы А (СДНФ А) – это дизъюнктивная нормальная форма, для которой выполняются свойства совершенства (С) и которая существует в единственном числе.

СДНФ А можно получить двумя способами:

а) с помощью таблицы истинности (см. выше);

б) с помощью равносильных преобразований.

Дата добавления: 2017-02-01