Конъюнктивная нормальная форма (КНФ) и совершенная конъюнктивная нормальная форма (СКНФ)

Решение

Пример 3.1

Правило получения СДНФ из формулы А с помощью равносильных преобразований.

1. Для формулы А получаем любую ДНФ А.

2. Из ДНФ А путем равносильных преобразований получаем СДНФ А, последовательно добиваясь выполнения четырех свойств СДНФ – свойств совершенства.

1) Пусть В есть слагаемое ДНФ А, не содержащее . Путем умножения В на равносильность заменяем его на два слагаемых, которые уже будут содержать переменную .

.

2) Если в ДНФ А входят два одинаковых слагаемых В, то лишнее можно отбросить, пользуясь равносильностью .

3) Если в некоторое слагаемое В в ДНФ А переменная входит дважды, то лишнюю переменную необходимо отбросить, учитывая равносильность .

4) Если в ДНФ А входит слагаемое В, содержащее конъюнкцию 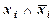, то это слагаемое можно отбросить, так как и тогда . Учитывая уже равносильность , где остальные слагаемые формулы А, слагаемое В можно отбросить.

Из формулы 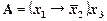получить СДНФ А с помощью таблицы истинности и с помощью равносильных преобразований.

1. Получение СДНФ А с помощью таблицы истинности.

Посколькуформула А содержит три переменные, то таблица истинности должна содержать строк.Составляем таблицу истинности

Таблица 3.3

Таблица истинности формулы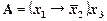

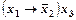
На тех наборах переменных, где формула принимает значение, равное 1, в качестве слагаемого запишем конъюнкцию элементарных переменных высказываний, взяв за член конъюнкции , если значение на указанном наборе переменных есть 1, и отрицание , если значение есть 0. Дизъюнкция всех записанных конъюнкций и будет искомой формулой. В нашем случае будем иметь

СДНФ А = .

Данная формула полностью отвечает свойствам совершенства.

2. Получение СДНФ А с помощью равносильных преобразований.

1) В соответствии с правилом получения СДНФ из формулы А с помощью равносильных преобразований для формулы А получаем любую ДНФ А.

.

2) Формула ДНФ А имеет два слагаемых, в каждом из которых недостает по одной переменной для того, чтобы она стала совершенной формой. Поэтому умножаем первое слагаемое на равносильность , чтобы получить недостающую переменную в двух новых слагаемых, а второе слагаемое на равносильность . Получим выражение

Приводим подобные члены (в выражении они подчеркнуты) и, пользуясь равносильностью, 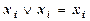отбрасываем лишнее слагаемое. Переставляя переменные в слагаемых по порядку возрастания, получим то же самое выражение, которое было получено с помощью таблицы истинности

СДНФ А = .

В тех случаях, когда в слагаемых полученной ДНФ А отсутствует одна или две переменные и когда переменных не больше четырех, для получения СДНФ А проще использовать равносильные преобразования, в противоположном случае - таблицу истинности.

Элементарной дизъюнкцией 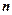переменных называется конъюнкция переменных или их отрицаний.

Элементарная конъюнкция 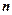переменных может быть записана в виде:

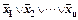или , или , или

и т. д.

Конъюнктивной нормальной формой формулы А называется равносильная ей формула, представляющая собой конъюнкцию дизъюнкций.

Конъюнкция элементарных дизъюнкций 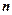переменных формулы А может быть записана в виде:

Совершенной конъюнктивной нормальной формой формулы А называется равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций.

Как и для ДНФ А, среди большого числа КНФ А существует единственная КНФ А, для которой выполняются перечисленные ранее четыре свойства совершенства, свойства (С). На этом основании можно дать следующее определение такой КНФ.

Совершенная конъюнктивная нормальная форма формулы А(СКНФ А) – это конъюнктивная нормальная форма, для которой выполняются свойства совершенства (С) и которая существует в единственном числе.

Правило получения СКНФ А с помощью таблицы истинности.

Если функция 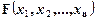задана таблицей истинности, то соответствующая ей СКНФ А может быть получена уже двумя способами.

1) СКНФ А получается так же, как и СДНФ А, но с использованием формулы . Для этого необходимо сначала получить с помощью таблицы , затем взять отрицание и использовать закон де Моргана для его снятия: .

2) При получении СКНФ А для каждого набора значений переменных, на котором функция 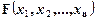принимает значение, равное 0, запишем дизъюнкцию элементарных переменных высказываний, взяв за член конъюнкции , если значение на указанном наборе значений переменных есть 0 и отрицание , если значение есть 1. Конъюнкция всех записанных дизъюнкций и будет искомой формулой.

Дата добавления: 2017-02-01