Замена плоскостей проекций

СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ

Примеры решения задач

8.3.1 Задание: опустить перпендикуляр из точки А на плоско­сть () и найти его основание точку В.

Решение: исходя из принципа перпендикулярности прямой и плоскости (прямая перпендикулярна к плоскости, если она перпенди­кулярна к двум пересекающимся прямым этой плоскости), необходи­мо в плоскости провести две пересекающиеся прямые, а именно гори­зонталь h и фронталь (рис. 8.9).

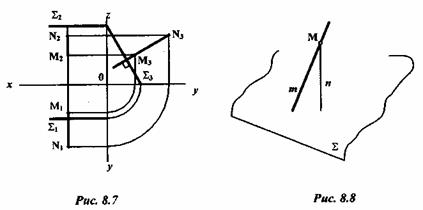
Затем из точки А проводим нормаль n к плоскости . На основа­нии теоремы о проецировании прямого угла и . Если плоскость задана следами, то и (рис. 8.10). Основание перпендикуляра определяется как точка пересечения его с плоско­стью. Для этого нужно провести через нормаль проецирующую плос­кость , найти линию пересечения l(l₁,l₂)плоскостей и и на пересечении этой линии и нормали отметить общую точку В для нормали и плоскости ().

Суть метода заключается в том, что одна из плоскостей проекций заменяется на новую плоскость проекций, при этом последнюю про­водят перпендикулярно к незаменяемой плоскости. При такой замене величина координаты любой точки на вводимой плоскости будет та­кой же, как координаты той же точки на заменяемой плоскости.

Например, если заменить фронтальную плоскость проекций П₂ на новую плоскость П₄ (рис. 9.1, а), то последняя должна быть перпен­дикулярна к плоскости П₁ а расстояние от проекции точки a₄ до оси x₁ будет равно расстоянию от проекции точки А₂ до оси х. Новая ось проекции х₁ проводится так, как этого требует решение задачи. В рас­сматриваемом случае она проведена произвольно.

При замене горизонтальной плоскости H₁ на новую плоскость П₅ (рис. 9.1, б) сохраняется неизменная координата.);.

При решении конкретной задачи таких замен может быть выпол­нено последовательно несколько. Главные условия этих действий — сохранение ортогонального проецирования в новой системе проекций и величин соответствующих координат.

Пусть дана прямая общего положения АВ (рис. 9.2). Необходимо преобразовать чертеж отрезка АВ таким образом, чтобы прямая стала проецирующей, т.е спроецировалась на одну из плоскостей проекции в точку. Такое преобразование с заменой плоскостей выполняется в два этапа.

На первом этапе новую плоскость, например П₄, вводят взамен фронтальной плоскости П₂, параллельно прямой АВ. Новую ось про­екций x₁ проводят параллельно горизонтальной проекции прямой A₁B₁. Далее проводят от горизонтальной проекции линии связи, пер­пендикулярные к новой оси проекций, и на них откладывают коорди­наты г, т.е. расстояние от сторон оси проекций до фронтальных про­екций точек. Новая проекция А₄В₄ будет определять натуральную длину отрезка АВ. Одновременно определяется угол наклона прямой к плоскости проекций, в рассматриваемом примере к горизонтальной плоскости П₁ – угол . При замене горизонтальной плоскости проек­ции П₁ на новую угол наклона прямой АВ к плоскости П₂ - .

На втором этапе в системе плоскостей П₁/П₄ плоскость проекций П₁ заменяют на П₅. При этом ось х₂ проводят перпендикулярно к про­екции А₄В₄. В новой системе плоскостей проекций П₄/П₅ прямая за­няла проецирующее положение, т.е. она стала перпендикулярна к плоскости П₅, и на нее прямая спроецировалась в точку, а концы от­резка АВ совпали на проекции А₅ В₅.

Метод применяется для определения расстояния между парал­лельными и скрещивающимися прямыми, величины двугранного уг­ла, натуральной величины плоской фигуры и различных ее парамет­ров.

В том случае, если прямые являются прямыми уровня, т.е. парал­лельны одной из плоскостей проекций, первый этап решения опуска­ется и преобразование начинается со второго этапа.

Дата добавления: 2017-02-01