
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Функция Лапласа
|
|
|
|
Правило 3-х сигм
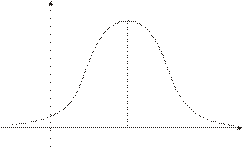
Нормальное (Гауссово) распределение
Квантили распределения
Свойства дисперсии
1. 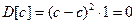
2. 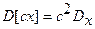
3. 
4. 
 - среднее квадратическое отклонение (в линейных единицах)
- среднее квадратическое отклонение (в линейных единицах)
 - коэффициент вариации (изменчивости) (в относительных единицах)
- коэффициент вариации (изменчивости) (в относительных единицах)
Замечание. Коэффициент вариации применяют при анализе риска инвестирования.
Удобная формула расчета дисперсии: 

 - центральный момент
- центральный момент  – того порядка
– того порядка

3.  - коэффициент асимметрии
- коэффициент асимметрии
4.  - эксцесс (коэффициент островершинности)
- эксцесс (коэффициент островершинности)

 н ормальное (Гауссово) распределение выступает в качестве
н ормальное (Гауссово) распределение выступает в качестве
меры (эталона):

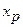 - квантиль уровня (вероятности)
- квантиль уровня (вероятности)  определяется как корень уравнения
определяется как корень уравнения  или, соответственно,
или, соответственно, 
Квантили:
 |
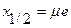 ; квартили;децили;процентили.
; квартили;децили;процентили.
(медиана)
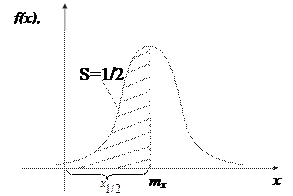 |
Квартили
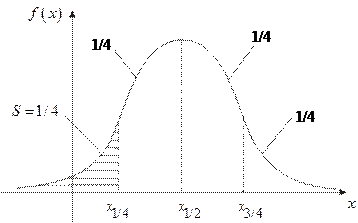 |
Квартили -  ; Децили -
; Децили - 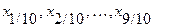 ; Процентили -
; Процентили -  .
.
Квантили широко используется в робастной статистике:
178; 187; 1655, 175; 178 
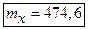 . Наблюдение 1655 – выброс (промах).
. Наблюдение 1655 – выброс (промах).
175; 178; 178; 187; 1655 
6. Мода распределения - 
| |||
 |
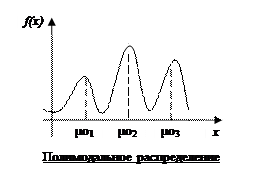

Пример использования моды: размеры одежды, перепись населения.
 |
 |
 ,
, 
 - двухпараметрическое распределение,
- двухпараметрическое распределение,
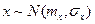 - обозначение с.в., имеющей нормальная распределение
- обозначение с.в., имеющей нормальная распределение
 -
- 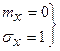 - обозначение с.в., имеющей нормированное
- обозначение с.в., имеющей нормированное
(стандартное) нормальное распределение
Операции нормирования и центрирования:



 ;
;




 |
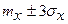 - зона практического рассеивания
- зона практического рассеивания
 - стандартное нормальное распределение с.в. от
- стандартное нормальное распределение с.в. от  до
до  . Проще рассматривать случай, когда
. Проще рассматривать случай, когда  .
.


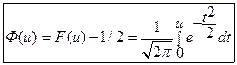
- табулированная функция Лапласа, широко используемая для определения вероятности попадания в диапазон значений:
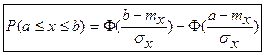 .
.
Роль нормального распределения. Теоретики и практики («мифы»).
Центральная теорема: Сумма конечного числа нормальных с.в. есть нормальная с. в.
Центральная предельная теорема: Сумма бесконечного числа с.в. с любыми законами распределения, но с примерно одинаковыми дисперсиями, имеет нормальное распределение.
Многие экономические показатели имеют нормальный или близкий к нормальному закон распределения: доход населения, прибыль фирмы в отрасли и др.
Пример. В результате длительных наблюдений определено, что дивиденды  и
и  по акциям фирм
по акциям фирм  и
и  являются нормальными с. в.:
являются нормальными с. в.:  ;
;  . Стоимость каждой акции равна 100$. Инвестор хочет приобрести акции на 1000 $.
. Стоимость каждой акции равна 100$. Инвестор хочет приобрести акции на 1000 $.
а)Какие законы распределения имеют доходы X, Y от вложения всей суммы в акции фирмы А или В? б)Каков закон распределения имеет доход Z от покупки акций в пропорции 2/3? в)Построить графики функций случайных величин X, Y, Z. г)Какова вероятность того, что полученный доход Z от вложения будет лежать в пределах от 110$ до 150$?
а) 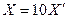
 X ~
X ~  (50;
(50; 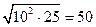 ) или
) или 
 Y ~
Y ~  (150,
(150,  );
);
б) 
 Z ~
Z ~  (mz=4
(mz=4  5+6
5+6  15=110, σz=
15=110, σz=  );
);
в) При построении графиков целесообразно пользоваться правилом 3-х сигм и обязательно соблюдать условие нормировки ( площадь под кривой распределения одна и та же - равна единице).
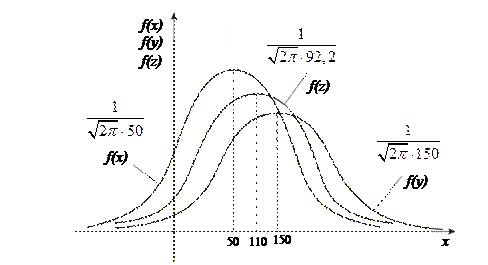
г)Р(110≤Z≤150)=Ф(0,43)-Ф(0)=0,16 (используются таблицы функции Лапласа).
Равномерное (равновероятное, прямоугольное)
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 128; Нарушение авторских прав?; Мы поможем в написании вашей работы!