
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Показательное (экспоненциальное) распределение
|
|
|
|
Распределение
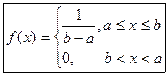



|


 - характеристическое свойство показательного распределения
- характеристическое свойство показательного распределения
Приложение - функция надежности. Пусть объект анализа начинает функционировать в момент времени  и по истечении
и по истечении 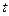 выходит из строя. Обозначим через
выходит из строя. Обозначим через  время безотказной работы. Тогда, вероятность отказа за время t равна:
время безотказной работы. Тогда, вероятность отказа за время t равна:

Для оценки вероятности безотказной работы («накапливающиеся отказы») часто используется экспоненциальное распределение. При этом параметр распределения λ=λ(t) является функцией времени. Технические системы, в демографии – смертность.

«Внезапные отказы» - Гамма – распределение.
Распределение χ2
Сумма квадратов  нормальных с.в.
нормальных с.в.  ~
~  (0,1)
(0,1)  является с.в.
является с.в.
и имеет табулированное распределение χ2 с  числом степеней свободы. Здесь
числом степеней свободы. Здесь  – число наложенных связей: обязательно - условие нормировки, и связи, связанные с расчетом тех или иных центральных или начальных моментов. Аналитическое выражение не приводится (сложное), распределение табулировано.
– число наложенных связей: обязательно - условие нормировки, и связи, связанные с расчетом тех или иных центральных или начальных моментов. Аналитическое выражение не приводится (сложное), распределение табулировано. 


t - распределение (Стьюдента)
 Если
Если  ~
~  (0,1), а
(0,1), а  ~χ2 с
~χ2 с  степенями свободы, то с.в.
степенями свободы, то с.в.  имеет распределение Стьюдента с
имеет распределение Стьюдента с  степенями свободы.
степенями свободы. 

 . Основное распределение малых выборок (до 15 -17 – ти наблюдений). Распределение табулировано
. Основное распределение малых выборок (до 15 -17 – ти наблюдений). Распределение табулировано
F - распределение (Фишера)
Если 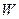 и
и  – независимые случайные величины, распределенные по закону χ2 с степенями свободы
– независимые случайные величины, распределенные по закону χ2 с степенями свободы  и
и  , соответственно, то с.в.
, соответственно, то с.в.
 имеет распределение Фишера (табулировано).
имеет распределение Фишера (табулировано).
В статистике широко используют прием введения некоторой случайной величины, распределение которой не зависит от числовых характеристик исходного анализируемого распределения. Такие величины имеют распределение Стьюдента, Фишера и  .
.
Двумерные с.в. («проклятие размерности»)
Уже было для событий и одномерных с.в.: 
|
 ;
; 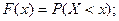


 - двумерные функция и ряд распределения
- двумерные функция и ряд распределения
  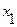
| 
| … | 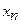
| |

| 
| 
| … | 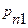
|

| 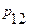
| 
| … | 
|
| … | … | … | … | … |

| 
| 
| … | 
|

 - условие нормировки,
- условие нормировки, 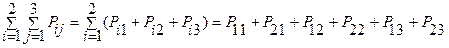
 ;
;  – поверхность,
– поверхность,  ≥ 0
≥ 0
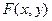 – неубывающая функция двух переменных, поверхность.
– неубывающая функция двух переменных, поверхность.
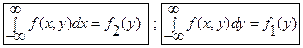 - получение одномерных плотностей
- получение одномерных плотностей
 - условие нормировки (единичный объем)
- условие нормировки (единичный объем)
 - для независимых с.в.
- для независимых с.в.
 - условные вероятности двумерной с.в.
- условные вероятности двумерной с.в.
|
 (сечения поверхности
(сечения поверхности  )
)
Двумерный закон распределения является исчерпывающей характеристикой, но сложен, поэтому используют числовые характеристики:
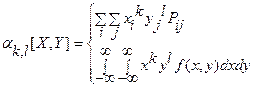 - начальный смешанный момент
- начальный смешанный момент
порядка 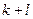
 - центральный смешанный момент
- центральный смешанный момент
порядка 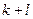
К орреляционный (взаимокорреляционный, кросскорреляционный)
момент (ковариация)
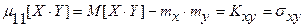

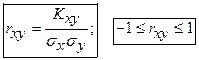 - коэффициент корреляции характеризует степень тесноты линейной связи.
- коэффициент корреляции характеризует степень тесноты линейной связи.


Свойства 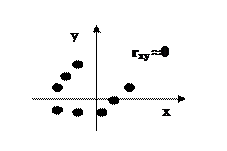
1)  ; 2)
; 2)  ;
;
3)если  и
и  независимы, то
независимы, то  0; но
0; но
если  0, то это не означает, что
0, то это не означает, что  и
и  независимы;
независимы;
4)  ;
;
5)если 
 - имеем детерминированную (функциональную) зависимость.
- имеем детерминированную (функциональную) зависимость.
Замечание: Из некоррелированности нормально распределенной двумерной случайной величины следует независимость переменных:.
Eсли 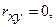 то
то

При  возможен другой (нелинейный) вид регрессии (стохастической связи), например,
возможен другой (нелинейный) вид регрессии (стохастической связи), например,  .
.
Условные математические ожидания (регрессии)

 .
.
Пример1. Дискретная двумерная с. в. задана таблицей распределения: Найти условное математическое ожидание с.в.  при значении с.в.
при значении с.в.  т.е.
т.е.  .
.
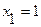
| 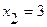
| 
| 
| |

| 0,15 | 0,06 | 0,25 | 0,04 |

| 0,3 | 0,1 | 0,03 | 0,07 |

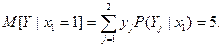
Пример регрессии X на Y. Условное математическое ожидание веса человека в функции от роста.

Пример регрессии Y на X. Расчет среднего роста человека при массе (весе) 75 кг. Задавая разные веса и рассчитывая средние статистические значения роста человека при данных весах получить стохастическую зависимость роста от веса.
Генеральная совокупность – одномоментно измеряют рост всего населения Земли (кто и как измеряет?). «Практические измерения – выборки – статистика».
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 72; Нарушение авторских прав?; Мы поможем в написании вашей работы!