Построение эмпирической (статистической) функция распределения

Основные понятия статистики

II. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Задачи математической статистики:

1)Указать способы сбора, группировки статистических методов, полученных в результате наблюдений или специально поставленных экспериментов.

2)Разработка методов анализа статистических характеристик в зависимости от цели исследования: оценка вероятности распределения, функции распределения, параметров функции распределения, зависимости случайной величины от одной или нескольких случайных величин.

Большинство решений по методам обработки статистических данных принимают до начала исследований, реже – в ходе исследования - «последовательный анализ» (примеры – приемочный контроль качества, статистическая физика).

Генеральная совокупность - объемом . Выборка – объемом (количество наблюдений для «разумного» результата). Репрезентативност ь (представительность) выборки.

Вероятность - неслучайная величина

-неслучайная функция.

В статистике частота 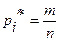- с. в.

Сходимость частоты по вероятности к вероятности:

- случайная функция,

г де -объем выборки, -число значений наблюдаемой выборки < .

Свойства эмпирической функции распределения

1) ;

2) - неубывающая функция;

3) если 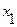- наименьшая варианта, ;

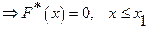4)если - наибольшая варианта, .

Пример. Построим эмпирическую функцию распределения для данного вариационного ряда:

	0,2	0,3	0,5

;

Пример. Построение полигона для следующего вариационного ряда:

	1,5	3,5	5,5	7,5
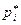
	0,1	0,2	0,4	0,3

ПолигонГистограмма

Пример. Построим гистограмму для выборки. Разбиваем интервал , в котором находятся все наблюдаемые значения, на несколько интервалов с шагом . В общем случае может быть различным. Подсчитываем - число значений выборки, попавших в - ый интервал (в случае попадания на границу интервала относят по влево и вправо). Подсчитываем частоты с.в. в -ом интервале: . Строим прямоугольники, у которых высоты равны 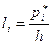; а площади равны .

Проверяем гипотезу о виде плотности распределения вероятностей (критерий Пирсона χ² ).

Для проверки гипотезы о виде интегральной функции распределения – используют критерии Романовского, Ястремского, Колмогорова.

Первым и необходимым этапом построения эмпирической функции распределения, гистограммы и расчета выборочных числовых характеристик распределения является обеспечение однородности выборки (устранение аномальных наблюдений).

Под аномальными наблюдениями понимают те отдельные наблюдения, которые не отвечают потенциальным возможностям исследуемой экономической (социально-экономической) системы и которые, оставаясь в выборке, оказывают существенное влияние на статистические характеристики выборки.

Возможные причины: ошибки при агрегировании и дезагрегировании экономических показателей, при передаче, при записи информации и т.д.

За показатель ошибочности отдельного наблюдения принимают значения его отклонения от остальных наблюдений: методы Ирвина, проверки разностей средних уровней, Фостера – Стьюдента, простой скользящей средней и экспоненциального сглаживания.

Методы обеспечения однородности обычно используют 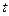распределение.

Наибольшее сомнение обычно вызывают несколько крайних значений вариационного ряда (левая и правая варианты).

Дата добавления: 2017-02-01