Свойства математического ожидания

Числовые характеристики распределения с.в.

Свойства плотности вероятности

Дифференциальный закон) распределения непрерывной с.в.

Плотность вероятности

Свойства функции распределения

.

Функция (интегральный закон) распределения с.в.

– является универсальной характеристикой и для непрерывных и для дискретных одномерных с.в. и описывает вероятность события :

Пример. Пусть случайная величина Х задана таблицей распределения (т.е. Х – дискретная случайная величина).

х
р	0,3	0,1	0,6

.

1. ;

2. ;

3. ;

4. - вероятность противоположного события;

5. - вероятность попадания в интервал значений.

х

6.

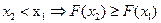
1. ;

2. - условие нормировки (единичная площадь под кривой распределения, полнота группы событий);

3. - выражение функции распределения через плотность;

4. - вероятность попадания в интервал значений.

Функции , , 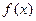ряды распределения исчерпывающим образом описывают одномерную с.в., однако они довольно сложны, а информация, содержащаяся в них, зачастую избыточна, поэтому широко используют числовые характеристики.

1. Математическое (безусловное) ожидание с.в.

, где - вероятность, а - элемент вероятности (вероятность попадания в ),

- оператор математического ожидания

- центр группирования, «среднее значение »,

центр тяжести плоской фигуры, ограниченной кривой .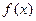

1.

2.

3. ;

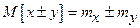4. ;

5. если и независимые с.в.

- начальный момент – того порядка

2. Дисперсия (безусловная) с.в.

- центрированная с.в.;

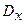- мера разброса (рассеяния) вокруг матожидания (в квадратных единицах), - оператор дисперсии

Дата добавления: 2017-02-01