Случайные одномерные величины

Интегральная формула Лапласа

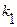Имеем вновь схему испытаний Бернулли, но требуется вычислить вероятность того, что событие появится в испытаниях от до 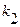раз (не менее 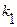и не более 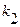раз). Эта задача распространена в прикладных вопросах теории вероятностей:

где - табулированная функция.

Пример. В страховой компании 10 000 клиентов. Страховой взнос – 2 000 руб. Вероятность страхового случая Страховая выплата – 200 000 руб. Определить размер прибыли стразовой компании с вероятностью

Прибыль млн. руб., где - число страховых случаев. Найдем такое , чтобы . .

Из таблицы найдем при 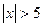. из таблиц 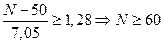. Окончательно млн. руб.

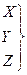случайные события, случайные величины (с.в.)

значения (в том числе и отрицательные) с.в. на числовой оси.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, априори неизвестное и независящее от случайных причин, которые заранее не могут быть учтены.

С.в. может быть непрерывной (аналоговой) или дискретной (прерывистой).

Пример непрерывной с.в.: расстояние, которое пролетает снаряд из орудия, зависит от большого количества факторов (ветра, t⁰, угла прицела, изменений количества и состояния пороха и т.д.), точности измерений (шаги, метры, микроны и т.д.). Имеет место и «эллипс» рассеяния (влево-вправо).

Непрерывная с.в. имеет бесконечное число значений и несчетна. Вероятность отдельного конкретного значения случайной величины равна 0 (но это событие возможно). Можно говорить о вероятности диапазона значений непрерывной с.в.

Дискретная с.в. может быть конечной или бесконечной, но она счетна (ей можно поставить в соответствие натуральный ряд чисел).

Примеры дискретной случайной величины:

1.Число родившихся мальчиков из 100 новорожденных случайно: 0, 1, 2, 3,... 100. Однако оно всегда дискретно и устойчиво больше, чем число родившихся девочек. С возрастом соотношение выравнивается, затем становится меньше.

2. Вероятность числа «успехов» в схеме Бернулли.

Характеристики с.в.: 1.Графики, таблицы.

2.Аналитические функции (интегральная и дифференциальная функция распределения), функционалы от них (числовые характеристики), квантили.

Дата добавления: 2017-02-01