Тема 1. Аналитическая геометрия на плоскости

УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ № 1

[1], с. 115 – 117, пример 4.12.

[5], с. 15 §2, с. 18 – 23 №78 – 98, §3 с.25 – 26 №128.

[7], с. 22 пример 1, с. 24 пример 1, с. 34 – 35 пример 1, с. 36 – 37 пример 1,

с. 39 – 40 пример 1, 2.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1. Даны вершины треугольника АВС: А(–4; 8), В(5; –4), С(10;6). Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС, и их угловые коэффициенты; 3) внутренний угол А с точностью до 0,01; 4) уравнение высоты СD и ее длину; 5) уравнение окружности, для которой высота СD есть диаметр; 6) систему линейных неравенств, определяющих треугольник АВС.

Решение. 1. Расстояние между точками и определяется по формуле:

Подставив в эту формулу координаты точек А и В, имеем:

2. Уравнение прямой, проходящей через точки и , имеет вид:

Подставив в (2) координаты точек А и В, получим уравнение прямой (АВ):

, записанное в общем виде. Для нахождения углового коэффициента прямой (АВ), разрешим полученное уравнение относительно : Тогда угловой коэффициент 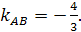Аналогично, подставив в формулу (2) координаты точек А и С, найдем уравнение прямой (АС).

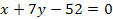
Для нахождения углового коэффициента 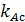прямой (АС), разрешим полученное уравнение относительно : Тогда

3. Угол между двумя прямыми, угловые коэффициенты которых равны определяются по формуле:

Угол А, образованный прямыми (АВ) и (АС), найдем по формуле (3), подставив в нее

4. Так как высота (CD) перпендикулярна стороне (АВ), то угловые коэффициенты этих прямых обратные по величине и противоположные по знаку, т.е.

Уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом 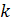, имеет вид:

Подставим в (4) координаты точки С и получим уравнение высоты (CD):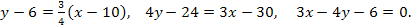

Для нахождения длины высоты (CD) воспользуемся формулой расстояния от точки до прямой ():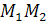

Определим расстояние от точки С(10;6) до прямой (АВ):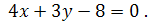

5. Уравнение окружности радиуса R с центром в точке имеет вид:

Так как высота (CD) является диаметром искомой окружности, то ее центр есть середина отрезка CD. Предварительно определим координаты точки D, как точки пересечения прямых (АВ) и (CD). Решим систему уравнений: ; откуда

Далее, используя формулы деления отрезка пополам, получим:

Следовательно, и Используя формулу (6), получим уравнение искомой окружности:

6. Множество точек треугольника АВС есть пересечение трех полуплоскостей, первая из которых ограничена прямой (АВ) и содержит точку С; вторая – ограничена прямой (ВС) и содержит точку А, третья полуплоскость ограничена прямой (АС) и содержит точку В.

Для получения неравенства, определяющего полуплоскость, ограниченную прямой АВ и содержащую точку С, подставим в уравнение прямой (АВ) координаты точки С:

Поэтому искомое неравенство примет вид:

Для составления неравенства, определяющего полуплоскость, ограниченную прямой (ВС) и содержащую точку А, прежде всего составим уравнение прямой (ВС), подставив в формулу (2) координаты точек В и С:

Подставив в полученное уравнение прямой (ВС) координаты точки А, имеем: Тогда искомое неравенство будет иметь вид:

Аналогично составим неравенство, определяющее полуплоскость, ограниченную прямой АС и содержащую точку В:

Третье искомое неравенство

Итак, множество точек треугольника АВС определяется системой неравенств:

На рис.1 в прямоугольной системе координат xOy изображен треугольник АВС, высота СD, окружность с центром в точке Е.

­ 4

В

Рис. 1.

Вопросы для самопроверки.

1. Дайте определение прямоугольной декартовой системы координат.

2. Напишите формулу для нахождения расстояния между двумя точками.

3. Напишите формулы для определения координат точки, делящей отрезок в заданном отношении; координаты середины отрезка.

4. Напишите уравнения прямой: а) с угловым коэффициентом; б) проходящей через данную точку в данном направлении; в) проходящей через две данные точки; г) в «отрезках» на осях.

5. Как определить координаты точки пересечения двух прямых?

6. Напишите формулу для определения угла между двумя прямыми.

7. Напишите условия параллельности и перпендикулярности двух прямых.

8. Напишите формулу расстояния от точки до прямой.

9. Сформулируйте определение окружности.

10. Напишите уравнение окружности с центром в любой точке плоскости ; с центром в начале координат.

Дата добавления: 2017-02-01