Тема 9. Определенный интеграл.

Решение.

Решение.

Выделим целую часть:

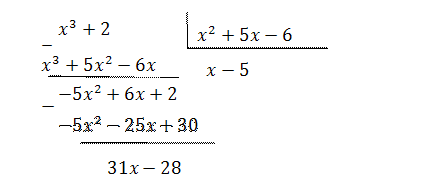
Итак, получаем

Разложим подынтегральную функцию на сумму простейших дробей:

Приведем правую часть к общему знаменателю:

Приравнивая числители, получаем

или Приравнивая справа и слева в полученном равенстве коэффициенты при одинаковых степенях 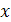, получим систему

Следовательно,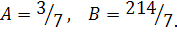

Вернемся к вычислению интеграла:

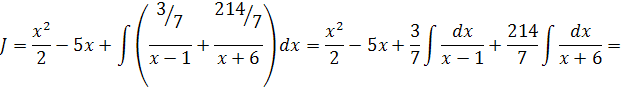
Рассмотрим случай, когда квадратный трехчлен знаменателя не имеет действительных корней. Основной прием вычисления такого интеграла состоит в том, что квадратный трехчлен дополняют до полного квадрата.

Задача 15. Вычислить интеграл:

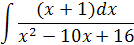
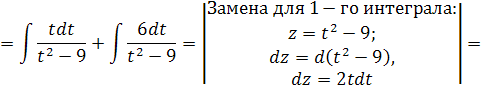
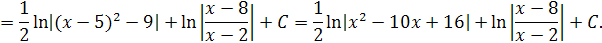
Вопросы для самопроверки

1. Сформулируйте определение первообразной функции.

2. Что называется неопределенным интегралом от данной функции?

3. Перечислите основные свойства неопределенного интеграла.

4. Напишите формулы таблицы основных интегралов.

5. В чем сущность метода интегрирования заменой переменной?

6. Напишите формулу интегрирования по частям в неопределенном интеграле.

[ 1] c. 296 пример 11.2 (а, б), с. 299 пример 11.4, с. 300 пример 11.5,

с. 301 – 302 пример 11.6, с. 304 пример 11.7, с. 305 – 307 примеры 11.8,

11.9, с. 308 пример 11.10, с. 311 пример 11.12, с. 315 – 318

примеры 11.14 – 11.17.

[5] c. 252 – 253 № 1592 – 1595, с. 254 – 255 № 1610 – 1612.

[11], с. 374 примеры 1 – 6, с. 375 пример 1, с. 379 – 380 примеры 1 – 3,

с. 401 – 402 примеры 1, 2, с. 403 примеры 3, 4, с. 407 пример 2.

При вычислении определенных интегралов применяют формулу Ньютона-Лейбница:

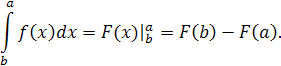
Покажем работу данной формулы на конкретных примерах.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 16. Вычислить интегралы:

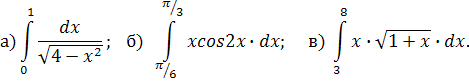
Дата добавления: 2017-02-01