Указания к выполнению контрольной работы №3.

Тема 11. Ряды.

[1] с. 357 – 358 примеры 13.1 – 13.3, с. 360 – 361 примеры 13.4, 13.5,

с. 363 – 365 примеры 13.6 – 13.8, с. 366 – 367 пример 13.9 (а, б),

с. 369 пример 13.10, с. 370 пример 13.11, с. 374 – 377

примеры 13.14 (а – д) – 13.15 (а – в), с. 381 – 383,

примеры 14.2 – 14.4, с. 389 пример 14.6 (д).

[2] c. 346 – 348 № 13.1 – 13.3, с. 350 – 355 № 13.14 (а – е) – 13.16,

с. 358 – 360 № 13.68 (а – в), с. 366 – 370 № 14.1 (а – е),

с. 376 – 378 № 14.28, с. 383 № 14.58 (е).

[12] c. 240 – 241 примеры 1,2, с. 243 – 244 примеры 1 – 5, с. 248 – 249

пример 1, с. 265 – 266 примеры 1 – 4, с. 277 § 21.

Числовым рядом называется бесконечная последовательность чисел, соединенных знаком сложения:

Сумма первых n членов ряда называется n-той частичной суммой ряда S_n.

Числа называются членами ряда, 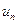- общим членом ряда.

Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е. .

Число S называется суммой ряда. Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.

Необходимое условие сходимости ряда. Если ряд - сходится, то .

Таким образом, если 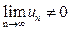, то ряд расходится.

Рассмотрим некоторые достаточные признаки сходимости и расходимости рядов.

Признак Даламбера. Пусть для ряда с положительными членами существует предел отношения . Тогда при 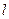<1 ряд сходится, при 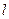>1 ряд расходится. При 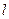=1 требуется дополнительное исследование для ответа на вопрос о сходимости ряда.

Интегральный признак сходимости ряда. Пусть дан знакоположительный ряд и пусть функция f(x) – такая, что f(1)=u₁, f(2)=u₂, …, f(n)=u_n, …- непрерывна и не возрастает при . Тогда для сходимости ряда необходимо и достаточно, чтобы сходился несобственный интеграл .

Ряд называется знакочередующимся, если его члены попеременно, то положительны, то отрицательны, .

Признак Лейбница. Если члены знакочередующегося ряда убывают по абсолютной величине, т.е. , и предел модуля его общего члена равен нулю, т.е. , то ряд сходится.

Степенным рядом называется ряд

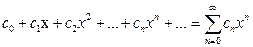
где с₀, с₁, …, с_n,.... – коэффициенты степенного ряда.

Радиус сходимости степенного ряда может быть найден по формуле:

. Интервал (-R, R) называется интервалом сходимости степенного ряда. При ряд может как сходиться, так и расходиться.

Интервал сходимости можно определять, применяя признак Даламбера, составленному из абсолютных величин членов исходного ряда. Записав ряд в виде: 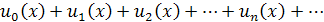, находят интервал сходимости из неравенства

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 20. Написать первые три члена ряда , найти интервал сходимости ряда и исследовать его сходимость на концах интервала.

Решение. Беря последовательно n=1, 2, 3, …, запишем данный ряд в виде:

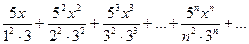
Для нахождения области сходимости ряда применим признак Даламбера.

Имеем, ; . Тогда получаем

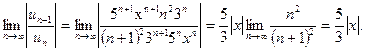
Данный ряд сходится абсолютно при тех значениях x, которые удовлетворяют неравенству

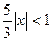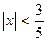, или , или .

Исследуем сходимость ряда на концах полученного интервала. При данный ряд принимает вид 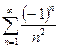. Ряд является знакочередующимся; абсолютная величина его общего члена стремится к нулю при 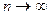. Следовательно, по признаку Лейбница сходимости знакочередующихся рядов этот ряд сходится. Значит, принадлежит области сходимости данного ряда.

При данный ряд принимает вид 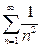. Исследуем сходимость этого ряда при помощи интегрального признака Коши. Рассмотрим несобственный интеграл

.

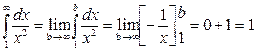Т.к. несобственный интеграл сходится, то сходится и исследуемый ряд. Значит, при исходный ряд сходится. Таким образом, 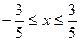- область сходимости данного ряда.

Задача 21. Вычислить с точностью до 0,001.

Решение. Если функция f(x) имеет производные любого порядка в окрестности точки x=0, то для функции f(x) может быть получен ряд Маклорена:

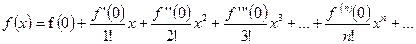
Используем разложение в ряд Маклорена для функции sinx:

.

Представим подынтегральную функцию в виде степенного ряда. Заменив x в разложении функции sin x на , имеем:

.

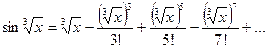Тогда

.

.

Полученный знакочередующийся ряд удовлетворяет условиям теоремы. Лейбница. Т.к. четвертый его член по абсолютной величине меньше 0,001, то для обеспечения заданной точности достаточно взять первые три члена. Тогда

.

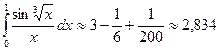Вопросы для самопроверки.

1. Что называется числовым рядом?

2. Что называется n-той частичной суммой числового ряда?

3. Какой числовой ряд называется сходящимся?

4. Что является необходимым условием сходимости числового ряда?

5. Назовите достаточные признаки сходимости, основанные на сравнении рядов.

6. Назовите признак Даламбера сходимости рядов.

7. В чем состоит интегральный признак сходимости Коши?

8. Какие ряды называются знакочередующимися? Приведите примеры.

9. Сформулируйте признак Лейбница сходимости знакочередующихся рядов.

10. Какие знакочередующиеся ряды называются абсолютно сходящимися? Условно сходящимися?

11. Дайте определение степенного ряда и области его сходимости.

12. Как найти область сходимости степенного ряда?

13. Запишите разложение в степенной ряд функций .

14. Как обеспечивается требуемая точность при применении степенных рядов в приближенных вычислениях?

Дата добавления: 2017-02-01