
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 10. Дифференциальные уравнения.
|
|
|
|
Решение.


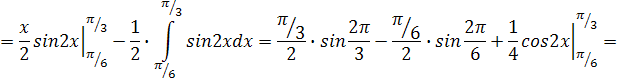
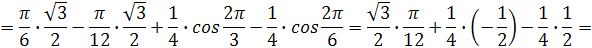


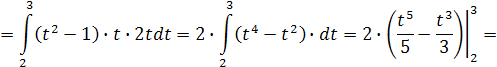

Задача 17. Вычислить площадь фигуры, ограниченной линиями:

Решение. Площадь 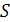 фигуры, ограниченная непрерывными линиями
фигуры, ограниченная непрерывными линиями
 ,
,  , при условии
, при условии 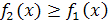 , определяется по формуле:
, определяется по формуле:
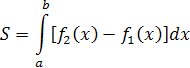
Для нахождения точек пересечения данных линий решаем систему уравнений
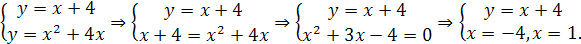
Итак, получили точки пересечения прямой и параболы: ( ;0) и (1; 5).
;0) и (1; 5).
Построим фигуру, ограниченную указанными линиями.
Тогда

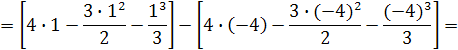


Рис. 6.
Вопросы для самопроверки
1. Назовите задачи, приводящие к понятию определенного интеграла.
2. Напишите интегральную сумму для функции  на отрезке
на отрезке 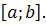
3. Что называется определенным интегралом от функции  на отрезке
на отрезке 
4. Каков геометрический смысл определенного интеграла?
5. Перечислите основные свойства определенного интеграла.
6. Чему равна производная от определенного интеграла с переменным верхним пределом интегрирования?
7. Напишите формулу Ньютона –Лейбница.
8. Напишите формулу интегрирования по частям в определенном интеграле.
9. Как вычистить объем тела, образованного вращением плоской фигуры вокруг оси 
10. Дайте определение несобственного интеграла с бесконечными пределами интегрирования.
11. Сформулируйте понятие несобственного интеграла от разрывной функции.
[1] с. 335 – 336 примеры 12.9 – 12.10, с. 338 пример 12.12,
с. 339 пример 12.13, с. 340 – 341 примеры 12.14 – 12.15, с. 344
пример 12.17 (а – в), с. 347 – 349 примеры 12.19 – 12.21, с. 350 – 354
примеры 12.23 – 12.24, задачи 1,2.
[6] c. 118 – 119 №507 – 510, с. 123 – 124 №545 – 547, с. 132 – 135
№596 – 602, с. 141 №649, с. 142 – 143 №656, с. 144 – 145 №666 – 667.
[12], с. 22 – 23, примеры 2 – 4, с. 25 пример 4, с. 30 – 31, пример 1,
с. 55 – 61 примеры 1 – 4, с. 70 § 21, с. 71 – 74 примеры 1 – 4.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 18. Решить уравнение 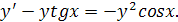
Решение. Данное уравнение является уравнением Бернулли, вид которого  Для его решения (как и для линейного уравнения) искомую функцию
Для его решения (как и для линейного уравнения) искомую функцию  представляем в виде произведения двух других функций:
представляем в виде произведения двух других функций:  то есть введем подстановку:
то есть введем подстановку: 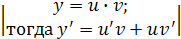 . Подставим данную замену в исходное дифференциальное уравнение, получим:
. Подставим данную замену в исходное дифференциальное уравнение, получим:

Сгруппируем второе и третье слагаемые:

Выберем функцию  так, чтобы
так, чтобы  . При подобном выборе функции
. При подобном выборе функции  уравнение (1) сведется к решению системы:
уравнение (1) сведется к решению системы:

Последовательно решаем уравнения (2) затем (3).
Решим уравнение (2):  данное уравнение – уравнение с разделяющимися переменными.
данное уравнение – уравнение с разделяющимися переменными.
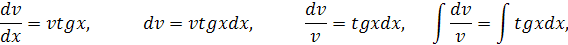


Подставляя найденную функцию  в уравнение (3), получаем:
в уравнение (3), получаем:



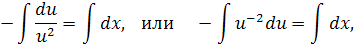

Тогда

Итак,

Задача 19. Найти частное решение уравнения

удовлетворяющее начальным условиям 
Решение. Общее решение  данного уравнения равно сумме общего решения
данного уравнения равно сумме общего решения 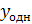 однородного уравнения и какого-либо частного решения
однородного уравнения и какого-либо частного решения  данного уравнения, то есть
данного уравнения, то есть 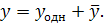
Для нахождения 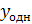 запишем однородное дифференциальное уравнение:
запишем однородное дифференциальное уравнение:  после этого составим соответствующее характеристическое уравнение:
после этого составим соответствующее характеристическое уравнение: 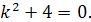 Данное уравнение имеет комплексные корни:
Данное уравнение имеет комплексные корни:  и
и  т.е.
т.е. 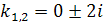 В этом случае общее решение однородного дифференциального уравнения имеет вид:
В этом случае общее решение однородного дифференциального уравнения имеет вид:

где  комплексные корни характеристического уравнения. Подставив в (4)
комплексные корни характеристического уравнения. Подставив в (4)  получаем:
получаем:
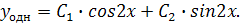
Для нахождения частного решения  неоднородного дифференциального уравнения воспользуемся следующей теоремой: если правая часть неоднородного уравнения есть функция
неоднородного дифференциального уравнения воспользуемся следующей теоремой: если правая часть неоднородного уравнения есть функция  и числа
и числа  не являются корнями характеристического уравнения
не являются корнями характеристического уравнения  , то существует частное решение
, то существует частное решение  Если же числа
Если же числа  являются корнями характеристического уравнения, то существует частное решение
являются корнями характеристического уравнения, то существует частное решение 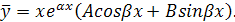
Применяя эту теорему при  имеем:
имеем:

Для нахождения коэффициентов  и
и  , дважды продифференцируем последнее равенство, получим:
, дважды продифференцируем последнее равенство, получим:
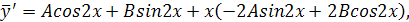
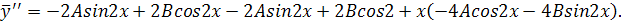

Подставим  и
и  в исходное уравнение:
в исходное уравнение:


или 
откуда получаем  Следовательно,
Следовательно,
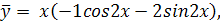
или  Тогда общее решение исходного дифференциального уравнения примет вид:
Тогда общее решение исходного дифференциального уравнения примет вид:

Для того чтобы записать частное решение, удовлетворяющее начальным условиям, необходимо найти  и
и  . Предварительно вычислим
. Предварительно вычислим 

Используя начальные условия, получим систему:

Следовательно,  есть искомое частное решение исходного дифференциального уравнения, удовлетворяющее заданным начальным условиям.
есть искомое частное решение исходного дифференциального уравнения, удовлетворяющее заданным начальным условиям.
Вопросы для самопроверки
1. Что называется дифференциальным уравнением?
2. Что называется общим решением дифференциального уравнения? Что называется частным решением?
3. Каков геометрический смысл частного решения дифференциального уравнения первого порядка?
4. Приведите примеры дифференциальных уравнений с разделяющимися переменными.
5. Какое дифференциальное уравнение первого порядка называется линейным? Уравнением Бернулли? Укажите способ их решения.
6. Какое уравнение называется линейным дифференциальным уравнением второго порядка с постоянными коэффициентами?
7. Какое уравнение называется характеристическим для однородного дифференциального уравнения второго порядка с постоянными коэффициентами?
8. Какой вид имеет общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами в зависимости от дискриминанта характеристического уравнения?
9. Как найти общее решение неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами? Какой вид имеет частное решение неоднородного дифференциального уравнения есть второго порядка с постоянными коэффициентами, если его правая часть многочлен? Показательная функция? Тригонометрическая функция?
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 88; Нарушение авторских прав?; Мы поможем в написании вашей работы!