Тема 5. Производная и дифференциал функции.

[1] c. 186 пример 7.7 (а – в), с. 190 пример 7.8 (а, б),

с. 199 примеры 7.11 – 7.12, с. 199 – 201 пример 7.13 (а – ж),

с. 202 пример 7.14 (а, б), с. 204 – 206 примеры 7.17 – 7.19.

[2], с. 188 – 190, № 7.13 (а – г) – 7.20, с. 199 – 202 № 7.131 – 7.136.

[5], с. 153 – 156 № 745 – 770, с. 159 № 896, 897, с. 160 № 908,

с. 166 № 975 – 981.

Для нахождения производной функции необходимо знать правила и формулы дифференцирования.

Правила дифференцирования:

произвольная константа; 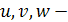некоторые дифференцируемые функции от

1.

2.

;

Теорема. Если и дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна

Формулы дифференцирования:

Пусть сложная функция от число

1.

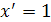
2.

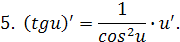
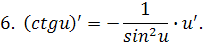
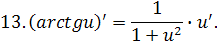
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 5. Определить производные функций:

Решение. а) Последовательно применяя формулы и правила дифференцирования, получим:

б)

в) В данном случае функциональная зависимость задана в неявном виде. Для нахождения производной надо продифференцировать по переменной 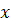обе части уравнения, считая при этом функцией от 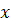, а затем полученное уравнение разрешить относительно

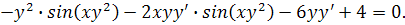
Из последнего равенства выражаем производную

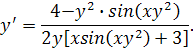
Вопросы для самопроверки

1. Что называется производной функции?

2. Каков геометрический, физический смысл производной?

3. Как взаимосвязаны непрерывность функции и ее дифференцируемость в точке?

4. Напишите основные правила дифференцирования.

5. Сформулируйте правило дифференцирования сложной функции.

6. Напишите формулы дифференцирования основных функций?

7. Что называется дифференциалом функции?

8. Каков геометрический смысл дифференциала функции.

9. Перечислите основные свойства дифференциала функции.

10. Напишите формулу, позволяющую находить приближенное значение функции при помощи ее дифференциала.

11. Как найти производную второго, третьего, n – го порядков?

12. Как вычислить дифференциал второго порядка от данной функции?

Тема 6. Приложения производной.

[1] c. 236 пример 8.16, с. 237 – 240 примеры 8.17 – 8.18,

с. 240 § 8.10.

[5] c. 176 – 177, № 1049 – 1054, с. 181 – 182 № 1096, 1097.

[11], с. 146 пример 1, с. 149 – 150 примеры 1 – 3, с. 153 – 154

примеры 1, 2, с. 155 – 158 примеры 1 – 4, с. 159 – 160 пример 1,

задачи 1, 2, с. 164 примеры 1 – 3, с. 165 – 167 примеры 4 – 6,

с. 168 примеры 1 – 3, с. 170 – 171 примеры 4, 5, с. 172 – 175

примеры 5 – 6.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 6. Исследовать функцию и построить ее график:

Решение. Исследование функции проведем по схеме:

1. Выяснить область определения функции.

2. Исследовать функцию на непрерывность.

3. Установить, является ли функция четной или нечетной.

4. Определить интервалы возрастания и убывания функции, найти точки экстремума.

5. Определить интервалы выпуклости, вогнутости кривой, выявить наличие точек перегиба.

6. Найти асимптоты кривой.

7. Определим точки пересечения функции с осями координат.

Реализуем указанную схему.

1. Функция определена при всех значениях аргумента 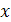, кроме т.е

2. Данная функция непрерывна на всей области определения, т.е. на интервалах (

3. Для установления четности или нечетности функции проверим выполнение равенства (тогда функция есть четная функция) или 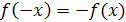(тогда есть нечетная функция) для любых 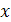и 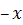из области определения функции:

Итак, получили, чт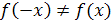о и , т.е. данная функция не является ни четной, ни нечетной.

4. Исследуем функцию на экстремум. Для этого из равенства определим критические точки.

Далее, приравняем производную к нулю:

Отсюда получаем критическую точку . На числовой оси отметим критическую точку и точку, не принадлежащую области определения функции. Получаем три интервала: Исследуем характер критической точки:

при 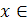имеем

при имеем

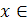
при имеем

Следовательно, при функция имеет минимум. Вычислим значение функции в точке минимума: Итак, точка А есть точка минимума.

Рис. 2.

Далее, по знаку первой производной выявим интервалы возрастания и убывания функции:

на интервалах 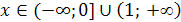имеем , следовательно, функция убывает;

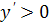на интервале имеем , следовательно, функция возрастает.

5. Для определения точек перегиба, интервалов выпуклости и вогнутости кривой найдем вторую производную:

Приравняем вторую производную к нулю и найдем точки, в которых вторая производная равна нулю или не существует:

получаем, что 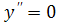при , т.е. является точкой, в которой возможен перегиб; и не существует при Но в точке функция не может иметь перегиб, т.к. данная точка не принадлежит области определения. Разобьем числовую ось на три интервала: Исследуем знак второй производной на каждом интервале:

при имеем , следовательно, кривая на этом интервале выпуклая;

при имеем , следовательно, кривая на этом интервале вогнутая;

при 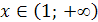имеем , следовательно, кривая на этом интервале вогнутая.

При переходе через точку вторая производная меняет знак, следовательно, точка является абсциссой точки перегиба. Вычислим значение функции в точке перегиба: 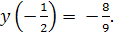Итак, точка В( есть точка перегиба функции.

Рис. 3.

6. Определим асимптоты кривой:

а) прямая является вертикальной асимптотой, так как в этой точке

б) для определения наклонной асимптоты воспользуемся формулами:

Тогда:

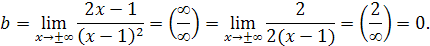
При вычислении последнего предела использовали правило Лопиталя. Таким образом, прямая есть горизонтальная асимптота.

7. Вычислим точки пересечения функции с осями координат.

При получаем при получаем

На основании проведенного исследования, построим график функции

Рис. 4.

Задача 7. Резервуар, имеющий форму открытого сверху прямоугольного параллелепипеда с квадратным дном, нужно вылудить внутри оловом. Каковы должны быть размеры резервуара при его емкости 108 л. воды, чтобы затраты на его лужение были наименьшими?

Решение. Затраты на покрытие резервуара оловом будут наименьшими, если при данной емкости его поверхность будет минимальной.

Обозначим через а – сторону основания, – высоту резервуара. Тогда площадь его поверхности равна , а объем Отсюда

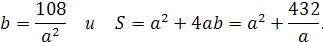
Полученное соотношение устанавливает зависимость между площадью поверхности резервуара 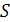(функция) и стороной основания а (аргумент). Исследуем функцию 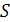на ее наименьшее значение в промежутке

Для этого сначала определим первую производную и приравняем ее к нулю. После чего решим полученное уравнение:

Отсюда Так как 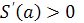при и как при , следовательно, при функция 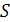имеет минимум. Заметив, что

т.е. при стремлении к нулю или бесконечности поверхность 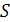неограниченно возрастает, мы приходим к выводу, что в точке функция 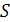имеет наименьшее значение.

Если , то 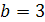. Таким образом, затраты на лужение резервуара емкостью 108 л. будут наименьшими, если он имеет размеры:

Вопросы для самопроверки

1. Сформулируйте теоремы Ролля, Лагранжа. Каков их геометрический смысл?

2. Какая функция является возрастающей, убывающей?

3. Сформулируйте признаки возрастания и убывания функции.

4. Какие точки называются критическими, какие точками экстремума?

5. Назовите необходимый и достаточный признаки экстремума функции.

6. Что называется выпуклостью и вогнутостью кривой?

7. Назовите признаки выпуклости и вогнутости кривой.

8. Сформулируйте достаточный признак существования точки перегиба кривой.

9. Что называется асимптотой кривой?. Как определить вертикальные и наклонные асимптоты кривой?

10. Сформулируйте правило Лопиталя. В каких случаях при вычислении пределов его можно применять?

Дата добавления: 2017-02-01