
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 7. Функции нескольких переменных.
|
|
|
|
[1] c. 405 пример 15.7 (а, б), с. 406 пример 15.8, с. 413 – 414 пример 15.9,
с. 414 пример 15.10, с. 428 § 15.11.
[2], с. 393 – 394, № 15.27, 15.28, с. 397 – 398 № 15.56 – 15.58, с. 409 – 411
№ 15.107 – 15.109.
[5], с. 193 – 194 № 1192 – 1196, с. 205 № 1305, 1306.
Пусть имеется две переменные величины, и каждому набору их значений 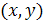 из некоторого множества X соответствует одно вполне определенное значение переменной величины z. Тогда говорят, что задана функция двух переменных
из некоторого множества X соответствует одно вполне определенное значение переменной величины z. Тогда говорят, что задана функция двух переменных 
Переменные 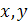 называются независимыми переменными или аргументами, z – зависимой переменной, а символ
называются независимыми переменными или аргументами, z – зависимой переменной, а символ  означает закон соответствия. Множество X называется областью определения функции.
означает закон соответствия. Множество X называется областью определения функции.
Зададим переменной 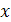 приращение
приращение  , оставляя переменную
, оставляя переменную  неизменной. Тогда разность
неизменной. Тогда разность  называется частным приращением функции
называется частным приращением функции  по переменной
по переменной 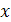 .
.
Зададим переменной  приращение
приращение  оставляя переменную
оставляя переменную 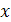 неизменной. Тогда разность
неизменной. Тогда разность  называется частным приращением функции
называется частным приращением функции  по переменной
по переменной 
Частной производной по  от функции
от функции  называется предел отношения частного приращения
называется предел отношения частного приращения 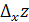 по
по 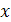 к приращению
к приращению  при стремлении
при стремлении  к нулю:
к нулю:

Частной производной по  от функции
от функции  называется предел отношения частного приращения
называется предел отношения частного приращения  по
по  к приращению
к приращению  при стремлении
при стремлении  к нулю:
к нулю:

Замечание. Если от функции  берется производная
берется производная  , то переменная
, то переменная  считается константой. Если же от функции
считается константой. Если же от функции  берется производная
берется производная  то переменная
то переменная 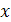 считается константой.
считается константой.
Для вычисления частных производных применяются те же правила и таблица, что и для функции одной переменной.
Определение. Точка  называется точкой максимума функции
называется точкой максимума функции  , если для любых
, если для любых  достаточно малых по абсолютной величине выполняется неравенство
достаточно малых по абсолютной величине выполняется неравенство 
По смыслу определения функция  должна иметь смысл на некотором множестве точек этой окрестности.
должна иметь смысл на некотором множестве точек этой окрестности.
Определение. Точка  называется точкой минимума функции
называется точкой минимума функции  , если для любых
, если для любых  достаточно малых по абсолютной величине выполняется неравенство
достаточно малых по абсолютной величине выполняется неравенство 
Теорема (необходимое условие экстремума). Если функция  достигает экстремума в точке
достигает экстремума в точке 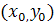 , то каждая частная производная первого порядка от функции
, то каждая частная производная первого порядка от функции  обращается в ноль в этой точке или не существует.
обращается в ноль в этой точке или не существует.
Определение. Точки, в которых  (или не существует) и
(или не существует) и  (или не существует), называются критическими точками функции
(или не существует), называются критическими точками функции 
Обозначим через А, В, С значения вторых частных производных в точке  :
:
А =  , В =
, В =  , С =
, С =  .
.
Достаточное условие экстремума сформулируем следующим образом.
Пусть в некоторой области, содержащей точку  функция
функция  имеет непрерывные частные производные до третьего порядка включительно; пусть точка
имеет непрерывные частные производные до третьего порядка включительно; пусть точка  является критической точкой функции
является критической точкой функции  , т.е.
, т.е.
 ,
, 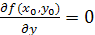 . Тогда при
. Тогда при 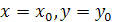 :
:
1)  имеет максимум, если
имеет максимум, если 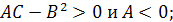
2)  имеет минимум, если
имеет минимум, если 
3)  не имеет ни максимума, ни минимума, если
не имеет ни максимума, ни минимума, если 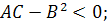
4) если  , то экстремум может быть и может не быть, т.е. вопрос об экстремуме в этом случае остается открытым.
, то экстремум может быть и может не быть, т.е. вопрос об экстремуме в этом случае остается открытым.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 8. Исследовать на экстремум функцию

Решение. 1) Найдем критические точки, пользуясь необходимыми условиями экстремума: 
Решая систему, получаем критическую точку (4;-2).
2) Найдем производные второго порядка в критической точке и определяем характер критической точки:
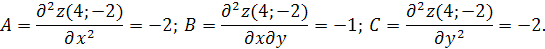
Получаем,  Так как
Так как  ,то в точке (4;-2) функция имеет максимум:
,то в точке (4;-2) функция имеет максимум:

Задача 9. Исследовать на экстремум функцию 
Решение. 1) Определим критические точки, пользуясь необходимыми условиями экстремума: 
Решив систему, получаем две критические точки M(1;1) и N(0;0).
1) Вычислим производные второго порядка:

2) Исследуем характер первой критической точки M(1;1):


Следовательно, в точке (1;1) данная функция имеет минимум. Вычислим значение функции в этой точке: 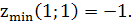
3) Исследуем характер второй критической точки N(0;0):

Следовательно, в точке (0;0) функция не имеет экстремума.
Определение. Наименьшее или наибольшее значение функции в данной области называется абсолютным экстремумом функции (соответственно абсолютным минимумом или абсолютным максимумом) в этой области.
Теорема. Абсолютный экстремум функции в данной области достигается либо в критической точке функции, принадлежащей этой области, либо в граничной точке области.
Чтобы выявить абсолютный экстремум функции в замкнутой области, необходимо:
1) определить критические точки, лежащие внутри области, и вычислить значения функции в этих точках; исследовать на экстремум эти точки не следует;
2) определить наибольшее и наименьшее значения функции на границе области; если граница состоит из нескольких линий, то исследование проводится для каждого участка в отдельности;
3) сравнить полученные значения функции и установить наибольшее и наименьшее значения функции в заданной замкнутой области.
Задача 10. Исследовать на абсолютный экстремум функцию
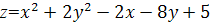 в замкнутом треугольнике, ограниченном прямыми
в замкнутом треугольнике, ограниченном прямыми 
 и
и  .
.
 Решение. 1. Определим критические точки, лежащие внутри заданной области – треугольник, заданный неравенствами
Решение. 1. Определим критические точки, лежащие внутри заданной области – треугольник, заданный неравенствами  . Для этого найдем частные производные первого порядка:
. Для этого найдем частные производные первого порядка:
 Приравняв частные производные к нулю, получаем следующую систему:
Приравняв частные производные к нулю, получаем следующую систему:  решив которую, определяем критическую точку М(1;2). Точка М лежит в заданной области. Вычислим значение функции в этой точке:
решив которую, определяем критическую точку М(1;2). Точка М лежит в заданной области. Вычислим значение функции в этой точке: 
2. Определим значения функции на границе области.
а) На отрезке ОА  , а
, а  Если
Если  , то
, то  Вычислим производную от полученной функции, после чего найдем ее критические точки:
Вычислим производную от полученной функции, после чего найдем ее критические точки:  Получили критическую точку N(1;0). Находим значения функции в критической точке и на концах отрезка [0;4]:
Получили критическую точку N(1;0). Находим значения функции в критической точке и на концах отрезка [0;4]: 
б) На отрезке ОВ  и
и  Если
Если  , то
, то 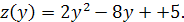 Вычислим производную от полученной функции, после чего найдем ее критическую точку:
Вычислим производную от полученной функции, после чего найдем ее критическую точку:  Получили критическую точку L(0;2). Находим значения функции в критической точке и на концах отрезка [0;4]:
Получили критическую точку L(0;2). Находим значения функции в критической точке и на концах отрезка [0;4]: 
в) Теперь исследуем функцию на границе АВ. Уравнение прямой АВ имеет вид  . Подставив это выражение для
. Подставив это выражение для  в заданную функцию
в заданную функцию  получим
получим  Вычислим производную от полученной функции, после чего найдем ее критическую точку:
Вычислим производную от полученной функции, после чего найдем ее критическую точку:  Получили критическую точку К(
Получили критическую точку К( Вычислим значение функции в точке К:
Вычислим значение функции в точке К:  Значения функции на концах отрезка АВ ранее определены.
Значения функции на концах отрезка АВ ранее определены.
3. Сравнивая полученные значения функции  в точках М, N, L, K, O, А, В, заключаем, что наибольшее значение в заданной замкнутой области функция
в точках М, N, L, K, O, А, В, заключаем, что наибольшее значение в заданной замкнутой области функция  имеет в точке А(4;0), а наименьшее значение имеет в точке М(1;2). Итак,
имеет в точке А(4;0), а наименьшее значение имеет в точке М(1;2). Итак, 
Вопросы для самопроверки
1. Дайте определение функции двух независимых переменных. Приведите примеры.
2. Что называется областью определения функции двух независимых переменных? Каково геометрическое изображение функции двух переменных?
3. Что называется частным и полным приращение функции двух независимых переменных?
4. Сформулируйте определение предела функции двух переменных.
5. Какая функция называется непрерывной в точке? В области?
6. Дайте определение частных производных первого порядка функции двух переменных. Каков их геометрический смысл?
7. Что называется полным дифференциалом функции двух переменных?
8. Как найти частные производные второго, третьего и т.д. порядков функции нескольких переменных?
9. Что является необходимым условием экстремума функции двух переменных?
10. Сформулируйте достаточный признак экстремума функции двух переменных.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 74; Нарушение авторских прав?; Мы поможем в написании вашей работы!