Тема 14. Элементы линейного программирования.

Решение.

Решение.

Решение.

Тема 13. Случайные величины и их характеристики.

[3] c. 66 пример 1, с. 67 – 68 пример 1, с. 69 пример 1, с. 76

примеры 1, 2, с. 89 пример 1, с. 115 пример 1, с. 117 пример 1,

с. 117 пример 1, с. 118 – 119 пример 1, с. 120 пример 1, с. 126 – 127

примеры 1, 2, с. 133 пример 1, с. 134 пример 1.

[4] с. 53 №164, с. 54 – 55 №170, с. 64 №188 (а), с. 71 №210, с. 91 – 93

№262, 267, с. 98 №280, с. 101 №295, с. 101 – 102 №297, с. 110

№328, с. 111 – 112 №334, 337.

[9] с. 89 – 90 примеры 3.1, 3.2, с. 95 – 96 примеры 3.5, 3.6, с. 100

пример 3.8, с. 104 – 105 пример 3.11, с. 110 пример 3.13,

с. 113 – 114 пример 3.14, с. 121 – 132 примеры 3.18 – 3.24 (а – д).

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 26. Задан закон распределения дискретной случайной величины X:

X
P	0,1	0,3	0,2	0,4

Определить: 1) математическое ожидание M(X); 2) дисперсию D(X); 3) среднее квадратическое отклонение .

1) Если закон распределения дискретной случайной величины задан таблицей

X			…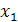
P			…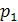

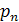
где в первой строке даны значения случайной величины X, а во второй – вероятности этих значений, то математическое ожидание M(X) вычисляется по формуле

.

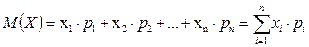Тогда .

2) Дисперсией D(X) дискретной случайной величины X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

.

Эта величина характеризует среднее ожидаемое значение квадрата отклонения X от M(X). Из последней формулы имеем:

.

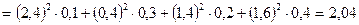Дисперсию D(X) можно определить другим способом, исходя из следующего свойства: дисперсия D(X) равна разности между математическим ожиданием квадрата случайной величины X и квадратом ее математического ожидания M(X), т.е.

.

Для вычисления составим следующий закон распределения величины :

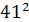
P	0,1	0,3	0,2	0,4

Тогда

и

.

3) Для характеристики рассеяния возможных значений случайной величины вокруг ее среднего значения вводится среднее квадратическое отклонение случайной величины X, равное квадратному корню из дисперсии D(X), т.е.

Из этой формулы следует: .

Задача 27. Непрерывная случайная величина X задана интегральной функцией распределения

Определить: 1) дифференциальную функцию распределения f(x); 2) математическое ожидание M(X); 3) дисперсию D(X).

1) Дифференциальной функцией распределения f(x) непрерывной случайной величины X называется производная от интегральной функции распределения F(x), т.е.

f(x) = .

Искомая дифференциальная функция имеет следующий вид:

2) Если непрерывная случайная величина X задана функцией f(x), то ее математическое ожидание определяется формулой

.

Т.к. функция f(x) при и при равна нулю, то из последней формулы получаем

.

3) Дисперсию D(X) определим по формуле

.

Тогда

.

Задача 28. Длина детали представляет собой нормально распределенную случайную величину с математическим ожиданием 40мм. и средним квадратическим отклонением 3 мм. Определить: 1) вероятность того, что длина произвольно взятой детали будет больше 34 мм. и меньше 43 мм.; 2) вероятность того, что длина детали отклонится от ее математического ожидания не более чем на 1,5 мм.

1) Пусть X – длина детали. Если случайная величина X задана дифференциальной функцией f(x), то вероятность того, что X примет значения, принадлежащие отрезку , определяется по формуле

.

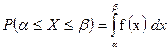Вероятность выполнения строгих неравенств определяется той же формулой. Если случайная величина X распределена по нормальному закону, то

,

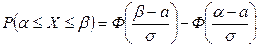где Ф(x) –функция Лапласа, а = M(X), .

В задаче а = 40, . Тогда

.

2) По условию задачи , где а = 40, . Подставляя эти значения в формулу попадания случайной величины в интервал для нормально распределенной случайной величины, получаем

, т.е.

.

Из этой формулы следует:

.

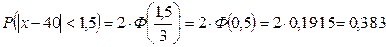Вопросы для самопроверки.

1. Какие случайные величины называются дискретными? Непрерывными? Приведите примеры.

2. Что называется законом распределения случайной величины? Как задается закон распределения дискретной случайной величины?

3. Что называется математическим ожиданием дискретной случайной величины? Ее дисперсией? Средним квадратическим отклонением? Перечислите их свойства.

4. Дайте определение интегральной функции распределения; дифференциальной функции распределения. Перечислите свойства этих функций.

5. Как вычисляются математическое ожидание и дисперсия непрерывной случайной величины?

6. Запищите дифференциальную функцию для нормального закона распределения.

7. Запишите формулу для определения вероятности попадания значений нормально распределенной случайной величины в заданный интервал.

8. Сформулируйте правило «трех сигм».

9. Назовите сущность закона больших чисел.

10. Запишите неравенство Чебышева.

11. Сформулируйте теорему Чебышева; теорему Бернулли.

[7] c. 71 – 75 задачи 1- 3.

[10] с. 540 §3, c. 542 пример 1.

[13] c. 419 §29, с. 421 – 424 №29.1 – 29.4.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 29. Предприятие имеет возможность приобрести не более 20 трехтонных и не более 18 пятитонных автомашин. Отпускная цена трехтонного грузовика 4 млн. руб., пятитонного – 5 млн. руб. Сколько нужно приобрести автомашин каждой марки, чтобы их суммарная грузоподъемность была максимальной, если для приобретения автомашин выделено 150 млн. рублей? Задачу решить графическим и аналитическим методами.

Дата добавления: 2017-02-01