При решении задач без вывода

Перечень формул, которые можно использовать

Физические основы классической механики

Мгновенная скорость материальной точки

,

где - радиус-вектор материальной точки.

Средняя скорость материальной точки

где - вектор перемещения материальной точки за интервал времени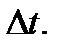

Средняя путевая скорость

где - путь, пройденный точкой за интервал времени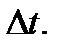

Ускорение материальной точки

Модуль нормального ускорения материальной точки при движении по криволинейной траектории

,

где R – радиус кривизны траектории в данной точке.

Модуль тангенциального ускорения материальной точки при движении по криволинейной траектории

.

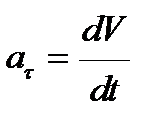Модуль средней угловой скорости материальной точки, совершающей вращательное движение

где - изменение угла поворота точки в радианах за интервал времени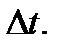

Модуль мгновенной угловой скорости вращательного движения материальной точки

Модуль углового ускорения материальной точки

Формулы связи между модулями линейных и угловых величин, характеризующих движение точки по окружности:

где V - модуль линейной скорости; а_t и а_n - модули тангенциального и нормального ускорений; w - модуль угловой скорости; e - модуль углового ускорения; R – радиус окружности.

Модуль полного ускорения

.

Первый закон Ньютона для замкнутой системы материальных точек:

.

Второй Закон Ньютона для поступательного движения:

или ,

где - сумма сил, действующих на материальную точку массы т, - импульс материальной точки.

Импульс материальной точки

.

Закон сохранения импульса для замкнутой системы материальных точек

.

Силы, рассматриваемые в механике:

а) проекция упругой силы на ось х

F_х=- kx,

где k – коэффициент упругости (в случае пружины жесткость); х – абсолютная деформация;

б) сила тяжести

,

в) сила гравитационного взаимодействия (закон всемирного тяготения)

,

где - гравитационная постоянная; т ₁ и т ₂ – массы взаимодействующих тел; r – расстояние между телами (тела рассматриваются как материальные точки). В случае гравитационного взаимодействия силу можно выразить так же через напряженность гравитационного поля:

.

Напряженность гравитационного поля, создаваемого Землей вблизи ее поверхности принято обозначать буквой Модуль напряженности или ускорение свободного падения вблизи поверхности Земли

где М_З – масса Земли, а R_З – ее радиус;

г) сила трения (скольжения)

где m - коэффициент трения; N – сила нормального давления.

Работа силы при элементарном перемещении

,

где a - угол между направлениями векторов и .

Работа силы при конечном перемещении точки из положения 1 в положение 2

.

Работа А, совершаемая результирующей силой, определяется как мера изменения кинетической энергии материальной точки:

Кинетическая энергия материальной точки

или .

Потенциальная энергия:

а) упругодеформированной пружины

,

где k – жесткость пружины, х – абсолютная деформация;

б) гравитационного взаимодействия

,

где g - гравитационная постоянная; т ₁ и т ₂ – массы взаимодействующих тел; r – расстояние между ними (тела рассматриваются как материальные точки);

в) тела, находящегося в однородном поле силы тяжести,

,

где g – ускорение свободного падения; h – высота поднятия тела над уровнем, принятым за нулевой (формула справедлива при h<<R _З, где R _З – радиус Земли).

Закон сохранения механической энергии:

,

где Е – полная энергия замкнутой системы, взаимодействующих тел.

Момент силы относительно произвольной точки О

,

где - радиус-вектор, направленный от точки О к точке приложения силы и лежащий в плоскости действия силы.

,

где a - угол между направлениями векторов и 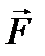; d – плечо силы – кратчайшее расстояние между точкой О и линией, вдоль которой действует сила.

Момент импульса материальной точки относительно произвольной точки О

, ,

где 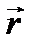- радиус-вектор от точки О к материальной точке по перпендикуляру, опущенному из рассматриваемой точки на ось; 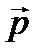- импульс материальной точки; a - угол между векторами и .

Момент инерции материальной точки массой т относительно оси вращения

,

где r – расстояние от точки до оси вращения.

Моменты инерции некоторых твердых тел массой т:

а) тонкого однородного стержня длиной l относительно оси, перпендикулярной стержню и проходящей через его центр масс:

;

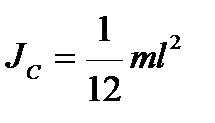б) обруча (тонкостенного полого цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью полого цилиндра)

,

где R – радиус обруча (цилиндра);

в) диска (сплошного однородного цилиндра) радиусом R относительно оси, перпендикулярной плоскости диска (сплошного цилиндра) и проходящей через его центр масс:

;

г) однородного шара радиусом R относительно оси, проходящей через центр масс шара

.

Теорема Штейнера:

,

где J – момент инерции тела относительно произвольной оси; J_C – момент инерции тела относительно оси, параллельной произвольной и проходящей через центр масс тела; d – расстояние между осями; т – масса тела.

Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси z:

,

где М_z – результирующий момент внешних сил относительно оси z, действующих на тело; e - угловое ускорение; J_z – момент инерции тела относительно оси вращения.

Кинетическая энергия тела, вращающегося вокруг неподвижной оси:

,

где J_z - момент инерции тела относительно оси z, w - угловая скорость.

Закон сохранения момента импульса системы тел, вращающихся вокруг неподвижной оси:

.

Кинематическое уравнение гармонических колебаний материальной точки:

,

где х – смещение точки из положения равновесия; А – амплитуда (максимальное смещение); w - циклическая частота; j - начальная фаза колебаний.

Скорость и ускорение материальной точки, совершающей гармонические колебания:

Сложение гармонических колебаний одного направления и одинаковой частоты:

а) амплитуда результирующего колебания

б) начальная фаза результирующего колебания

Связь периода колебаний маятника с частотой n:

.

Приведенная длина физического маятника

,

где J – момент инерции физического маятника относительно оси вращения; d – расстояние от оси до центра масс тела.

Периоды колебаний:

а) физического маятника

,

где L – приведенная длина физического маятника; g – ускорение свободного падения; J – момент инерции маятника относительно оси вращения; d – расстояние между точкой подвеса, через которую проходит ось вращения, и центром масс маятника; m – масса маятника;

б) математического маятника

,

где l – длина математического маятника;

в) пружинного маятника

,

где т – масса груза, k – коэффициент жесткости пружины.

Полная энергия тела, совершающего гармонические колебания

.

Потенциальная энергия упругодеформированного тела

.

Дата добавления: 2017-02-01