Молекулярная физика и термодинамика

Задачи

Таблица вариантов к контрольной работе №1

Вариант	Номера задач

Темы задач (для каждого варианта): в первой задаче – кинематика поступательного движения; во второй – кинематика криволинейного движения; в третьей – динамика поступательного движения; в четвертой – закон сохранения импульса; в пятой – закон сохранения механической энергии, работа механической силы; в шестой – динамика вращательного движения; в седьмой – закон сохранения момента импульса, кинетическая энергия вращательного движения; в восьмой – механические гармонические колебания.

101. Материальная точка движется прямолинейно с ускорением 5м/с². Определить, на сколько путь, пройденный в n -ю секунду, будет больше пути, пройденного в предыдущую секунду.

102. Две автомашины движутся по дорогам, угол между которыми α = 90^о. Скорость автомашин V ₁ = 20 м/с и V ₂ = 30 м/с. С какой скоростью V машины удаляются одна от другой?

103. Материальная точка движется в плоскости ху согласно уравнениям и где В ₁=7 м/с, С ₁ = -2 м/с, В ₂ = -1 м/с, С ₂ = 0,2 м/с². Найти модули скорости и ускорения точки в момент времени t = 5 c.

104. Одну треть своего пути автомобиль прошел со скоростью 18 м/с, остальную часть пути со скоростью 24 м/с. Какова средняя путевая скорость < V > автомобиля?

105. Рядом с поездом на одной линии с передними буферами тепловоза стоит человек. В тот момент, когда поезд начал двигаться с ускорением а = 0,1 м/с², человек начал бежать в том же направлении со скоростью V = 2,5 м/с. Через какое время t поезд нагонит человека? Определить скорость поезда в этот момент и путь, пройденный человеком.

106. Точка движется по прямой согласно уравнению 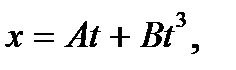где А = 6 м/с, В = -0,125 м/с³. Определить среднюю путевую скорость точки в интервале времени от t ₁=3 c до t ₂ =7 c.

107. Найти скорость V и ускорение а точки, движущейся прямолинейно, в момент времени t = 4 c. Движение точки описывается уравнением .

108. Зависимость пройденного телом пути s от времени t дается уравнением , где С = 0,14 м/с² и D = 0,01 м/с³. Через сколько времени после начала движения ускорение тела a станет равным 1 м/c²?

109. Пистолетная пуля пробила два вертикально расположенных листа бумаги, расстояние L между которыми равно 30 м. Пробоина во втором листе оказалась на h = 10 см ниже, чем в первом. Определить скорость V пули, если к первому листу она подлетела, двигаясь горизонтально. Сопротивлением воздуха пренебречь.

110. Камень падает с высоты h = 12 м. Какой путь s пройдет камень за последнюю секунду своего падения?

111. Колесо радиусом R = 0,4 м вращается так, что зависимость угла поворота колеса от времени определяется уравнением , где А = 2,5 рад, В = 2 рад/с, С = 1 рад/с³. Для точек, лежащих на ободе колеса, через 2 с после начала движения найти: 1) угловую скорость, 2) линейную скорость, 3) угловое ускорение, 4) тангенциальное ускорение, 5) нормальное ускорение, 6) полное ускорение.

112. Тело вращается вокруг неподвижной оси по закону: 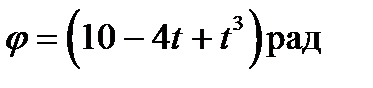. В какой момент времени угловая скорость вращения w будет равна 12 рад/с? Чему равно угловое ускорение e в этот момент времени?

113. Вентилятор вращается с частотой n = 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до полной остановки N =75 оборотов. Сколько времени прошло с момента выключения вентилятора до полной его остановки?

114. Колесо радиусом R = 10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе колеса, от времени движения определяется уравнением , где А = 3 см/с² и В = 1 см/с². Найти угол, составляемый вектором полного ускорения с радиусом колеса в момент времени t = 4 с после начала движения.

115. Диск радиусом R = 20 см вращается согласно уравнению , где А = 3 рад, В = 1 рад/с, С = 0,1 рад/с³. Для момента времени t = 10 с найти тангенциальное а_t, нормальное а_n и полное a ускорения точек на ободе диска.

116. На цилиндр, который может вращаться около горизонтальной оси, намотана нить. К концу нити привязали грузик и предоставили ему возможность опускаться. Двигаясь равноускоренно, грузик за время t = 3 c опустился на h = 1,5 м. Определить угловое ускорение e цилиндра, если его радиус r = 4 см.

117. Камень брошен с вышки в горизонтальном направлении с начальной скоростью V _o = 30 м/с. Определить скорость V, тангенциальное а_τ и нормальное а_n ускорения камня в конце второй секунды после начала движения.

118. Тело брошено под углом a = 30⁰ к горизонту. Найти тангенциальное а_τ, нормальное а_n ускорения тела в начальный момент движения.

119. Маховик начал вращаться равноускоренно и за промежуток времени t = 10 с достиг частоты вращения n = 300 мин^-1. Определить угловое ускорение ε маховика и число N оборотов, которое он сделал за это время.

120. Колесо автомашины вращается равноускоренно. Сделав N = 50 полных оборотов, оно изменило частоту вращения от n ₁= 4 c^-1 до n ₂= 6 c^-1. Определить угловое ускорение ε колеса.

121. Тело скользит по наклонной плоскости, составляющей с горизонтом угол a = 45⁰. Пройдя расстояние s = 36,4 см, тело приобретает скорость V = 2 м/с. Определить коэффициент трения m тела о плоскость.

122. Тело скользит по наклонной плоскости, составляющей с горизонтом угол a = 45⁰. Зависимость пути, пройденного этим телом, от времени дается уравнением s = Ct ², где С = 1,73 м/с². Найти коэффициент трения m тела о плоскость.

123. Найти силу тяги, развиваемую мотором автомобиля, движущегося в гору с ускорением a = 1 м/с². Уклон горы составляет 1 м на каждые 25 м пути. Масса автомобиля m = 9,8 т. Коэффициент трения m = 0,3.

124. К нити подвешен груз массой m = 1 кг. Найти натяжение нити, если нить с грузом: 1) поднимать с ускорением 5 м/с², 2) опускать с тем же ускорением.

125. Масса пассажирского лифта вместе с пассажирами составляет m = 800 кг. Найти, с каким ускорением, и в каком направлении движется лифт, если известно, что сила натяжения троса, поддерживающего лифт, равна: 1) 12000 Н; 2) 6000 Н.

126. Какую силу надо приложить к вагону, стоящему на рельсах, чтобы вагон начал двигаться равноускоренно и за время t = 30 с прошел путь s = 11 км? Масса вагона m = 16 т. Во время движения вагона на него действует сила трения, равная 0,05 веса вагона.

127. Грузик, привязанный к нити длиной l = 1 м, описывает окружность в горизонтальной плоскости. Определить период Т обращения, если нить отклонена на угол φ = 60⁰ от вертикали.

128. Автомобиль массой m = 5 т движется со скоростью V = 10 м/с по выпуклому мосту. Определить силу давления автомобиля на мост в его верхней части, если радиус кривизны моста R = 50 м.

129. Тело массой m = 0,5 кг движется прямолинейно, причем зависимость пройденного телом пути s от времени t дается уравнением , где С = 5 м/с² и D = 1 м/с³. Найти модуль силы, действующей на тело в конце первой секунды движения.

130. Под действием постоянной силы F = 10 H тело движется прямолинейно так, что зависимость пройденного телом пути s от времени t дается уравнением , где С =1 м/с². Найти массу m тела.

131. При горизонтальном полете со скоростью V = 250 м/с снаряд массой m = 8 кг разорвался на две части. Большая часть массой m ₁ = 6 кг получила скорость V ₁ = 400 м/с в направлении полета снаряда. Определить модуль и направление скорости V ₂ меньшей части снаряда.

132. Человек массой m ₁ = 70 кг, бегущий со скоростью V ₁ = 9 км/ч, догоняет тележку массой m ₂ = 190 кг, движущуюся со скоростью V ₂ = 3,6 км/ч, и вскакивает на нее. С какой скоростью станет двигаться тележка с человеком? С какой скоростью будет двигаться тележка с человеком, если человек до прыжка бежал навстречу тележке?

133. Конькобежец, стоя на коньках на льду, бросает камень массой m ₁ = 2,5 кг под углом α = 30⁰ к горизонту со скоростью V = 10 м/с. Какой будет начальная скорость V _o движения конькобежца, если масса его m = 60 кг? Перемещением конькобежца во время броска пренебречь.

134. На сколько переместится относительно берега лодка длиной L = 3,5 м и массой m ₁ = 200 кг, если стоящий на корме человек массой m ₂ = 80 кг переместится на нос лодки? Считать лодку расположенной перпендикулярно берегу.

135. В деревянный шар массой m ₁ = 8 кг, подвешенный на нити длиной l = 1,8 м, попадает горизонтально летящая пуля массой m ₂ = 4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол α = 3⁰? Удар пули считать прямым, центральным.

136. Какое количество энергии пошло на деформацию двух столкнувшихся шаров массами по 4 кг, если они двигались навстречу друг другу со скоростями V ₁ = 3 м/с и V ₂ = 8 м/с, а удар был прямым и неупругим?

137. Шарик массой m = 100 г упал с высоты h = 2,5 м на горизонтальную плиту, масса которой много больше массы шарика и отскочил от нее вверх. Считая удар абсолютно упругим, определить импульс, полученный плитой.

138. Из орудия массой M = 5000 кг вылетает снаряд массой m = 100 кг. Кинетическая энергия снаряда при вылете составляет 7,5 МДж. Какую кинетическую энергию получает орудие вследствие отдачи?

139. Шар массой m ₁ = 3 кг движется со скоростью V ₁ = 2 м/с и сталкивается с покоящимся шаром массой m ₂ = 5 кг. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.

140. Из ствола автоматического пистолета вылетает пуля массой m ₁ = 10 г со скоростью V = 300 м/с. Затвор пистолета массой m ₂ = 200 г прижимается к стволу пружиной, жесткость которой k = 25 кН/м. На какое расстояние отойдет затвор после выстрела? Считать, что пистолет жестко закреплен.

141. С какой наименьшей высоты h должен начать скатываться акробат на велосипеде (не работая ногами), чтобы проехать по дорожке, имеющей форму «мертвой петли» радиусом R = 4 м, и не оторваться от дорожки в верхней точке петли? Трением пренебречь.

142. На какую высоту h над поверхностью Земли поднимется ракета, пущенная вертикально вверх, если начальная скорость ракеты равна первой космической скорости V _I = 7,9 км/с?

143. Две пружины с жесткостями k ₁=0,3 кН/м и k ₂= 0,5 кН/м скреплены последовательно и растянуты так, что абсолютная деформация x ₂ второй пружины равна 3 см. Вычислить работу А растяжения пружин.

144. Налетев на пружинный буфер, вагон массой m = 16 т, двигавшийся со скоростью V = 0,6 м/с, остановился, сжав пружину на x = 8 см. Найти общую жесткость k пружин буфера.

145. Вычислить работу А, совершаемую на пути s = 12 м, силой, изменяющейся по закону F = (10 + 3 s)Н и совпадающей по направлению с перемещением.

146. Вычислить работу А, совершаемую при равноускоренном подъеме груза массой m = 100 кг на высоту h = 4 м за время t = 2 с.

147. Какую начальную скорость следует сообщить ракете, пущенной с поверхности Земли вертикально вверх, чтобы она поднялась на высоту h, равную двум радиусам Земли?

148. При подъеме груза массой m = 2 кг на высоту h = 1 м сила F совершает работу А = 78,5 Дж. С каким ускорением поднимается груз?

149. Пружина жесткостью k = 1 кН/м была сжата на х ₁ = 4 см. Какую нужно совершить работу А, чтобы сжатие пружины увеличить до х ₂ = 18 см?

150. Найти работу А подъема груза по наклонной плоскости длиной l = 2 м, если масса груза m = 100 кг, угол наклона φ = 30⁰, коэффициент трения μ = 0,1 и груз движется с ускорением а = 1 м/с.

151. К ободу сплошного однородного диска радиусом R = 0,2 м приложена постоянная касательная сила F = 98 Н. При вращении на диск действует момент сил трения М _тр = 5 Н×м. Найти массу m диска, если известно, что диск вращается с постоянным угловым ускорением ε = 10 с^-2_.

152. На горизонтальную ось насажены маховик и легкий шкив радиусом R = 5 см. На шкив намотан шнур, к которому привязан груз массой m = 0,4 кг. Опускаясь равноускоренно, груз прошел расстояние s = 1,8 м за время t = 3 с. Определить момент инерции маховика. Массу шкива считать пренебрежимо малой.

153. Шар массой m = 10 кг и радиусом R = 20 см вращается вокруг оси, проходящей через его центр. Уравнение вращения шара имеет вид , где В = 4 рад/с², С = -1рад/с³. Определить момент сил, приложенных к шару, в момент времени t = 2 с.

154. Через неподвижный блок массой m = 0,2 кг перекинут шнур, к концам которого подвесили грузы массами m ₁ = 0,3 кг и m ₂ = 0,5 кг. Определить силы натяжения шнура Т ₁ и Т ₂ по обе стороны блока во время движения грузов, если масса блока равномерно распределена по ободу.

155. Блок, имеющий форму диска массой m = 0,4 кг, вращается под действием сил натяжения нити, к концам которой подвешены грузы массами m ₁ = 0,3 кг и m ₂ = 0,7 кг. Определить силы натяжения Т ₁ и Т ₂ нити по обе стороны блока.

156. На обод маховика диаметром D = 60 см намотан шнур, к концу которого привязан груз массой m = 2 кг. Определить момент инерции маховика J, если он, вращаясь равноускоренно, под действием силы тяжести груза, за время t = 3 с приобрел угловую скорость ω = 9 рад/с.

157. Вал массой m = 100 кг и радиусом R = 5 cм вращался с частотой n = 8 с^-1. К цилиндрической поверхности вала прижали с силой F = 40 Н тормозную колодку, под действием которой вал спустя 10 с остановился. Определить коэффициент трения μ между валом и тормозной колодкой.

158. Через блок в виде сплошного диска, имеющего массу m = 1,5 кг, перекинута невесомая нерастяжимая нить, к концам которой подвешены грузы массами m ₁ = 0,1 кг и m ₂ = 0,2 кг. Определить ускорение движения грузов, если их предоставить самим себе.

159. Однородный стержень длиной l = 50 см и массой m = 400 г вращается с угловым ускорением ε = 3 с^–2 около оси, проходящей перпендикулярно стержню через его середину. Определить вращающий момент М.

160. На барабан массой m ₁ = 9 кг намотан шнур, к концу которого привязан груз массой m ₂ = 2 кг. Найти ускорение груза. Барабан считать однородным цилиндром. Трением пренебречь.

161. Шарик массой m = 60 г, привязанный к концу нити длиной l ₁ = 1,2 м, вращается с частотой n ₁ = 2 с^-1_, опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик к оси до расстояния l ₂ = 0,6 м. С какой частотой n ₂ будет при этом вращаться шарик? Какую работу А совершает внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь. Шарик рассматривать как материальную точку.

162. Платформа в виде диска радиусом R = 1 м вращается по инерции с частотой n ₁ = 6 об/мин. На краю платформы стоит человек, масса которого m = 80 кг. С какой частотой n ₂ будет вращаться платформа, если человек перейдет в ее центр? Момент инерции J платформы равен 120 кг×м². Момент инерции человека рассчитывать как для материальной точки.

163. Карандаш длиной l = 15 см поставленный вертикально, падает на стол без проскальзывания. Какую угловую скорость ω и линейную скорость V будет иметь в конце падения середина и верхний конец карандаша.

164. Горизонтальная платформа массой m = 80 кг и радиусом R = 1 м вращается с частотой n ₁ = 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой n ₂, будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от J ₁ = 3 кг∙м² до J ₂ = 1 кг∙м²? Считать платформу однородным диском.

165. По горизонтальной плоскости катится сплошной однородный диск со скоростью V =8 м/с. Определить коэффициент трения m, если диск, двигаясь по инерции, пройдет путь s =18 м.

166. Шар катится без скольжения по горизонтальной поверхности. Полная кинетическая энергия Е _кшара равна 14 Дж. Определить кинетическую энергию Е _{к пост} поступательного и Е _{к вр} вращательного движения шара.

167. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек. На какой угол φ повернется платформа, если человек пойдет вдоль края платформы и, обойдя ее, вернется в исходную на платформе точку? Масса платформы m =280 кг, масса человека m ₂ =80 кг.

168. С какой скоростью скатится без скольжения с наклонной плоскости высотой h = 2 м полый тонкостенный цилиндр?

169. На краю неподвижной скамьи Жуковского диаметром D = 3,8 м и массой m ₁ = 60 кг стоит человек массой m ₂ = 60 кг. С какой угловой скоростью ω начнет вращаться скамья, если человек поймает летящий на него мяч массой m = 0,5 кг со скоростью V = 5 м/с? Траектория мяча горизонтальна и проходит на расстоянии r = 1,9 м от оси скамьи. Момент инерции человека рассчитывать как для материальной точки.

170. Тонкий однородный стержень длиной l = 1,4 м может вращаться около горизонтальной оси, проходящей через конец стержня перпендикулярно его длине. Стержень отклонили на угол a = 90⁰ и отпустили. С какой угловой скоростью ω стержень будет проходить через положение равновесия?

171. Тело, подвешенное к цилиндрической пружине, растянуло ее на х _о = 5 см. Затем тело было смещено из положения равновесия по вертикали и отпущено, в результате чего оно стало совершать колебания. Найти период этих колебаний.

172. Точка совершает гармонические колебания с максимальной скоростью V _max = 10 см/с и максимальным ускорением а _max = 100 см/с². Найти циклическую частоту колебаний ω, период Т и амплитуду А. Написать уравнение колебания, приняв начальную фазу равной нулю.

173. Через какое время от начала движения точка, совершающая гармонические колебания, сместится от положения равновесия на половину амплитуды? Период колебаний Т = 24 с, начальная фаза φ = 0.

174. Уравнение колебаний материальной точки массой m = 16 кг имеет вид х = 0,1×sin(5πt/8+π/4) м. Найти величину максимальной силы F _max, действующей на точку, и полную энергию Е колеблющейся точки.

175. Определить частоту n гармонических колебаний сплошного однородного диска радиусом R = 20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.

176. Амплитуда гармонических колебаний материальной точки А = 2 см, а полная энергия колебаний Е = 0,3 мкДж. При каком смещении от положения равновесия на колеблющуюся точку действует сила F = 22,5 мкН?

177. На гладком горизонтальном столе лежит шар массой М = 200 г, прикрепленный к горизонтально расположенной легкой пружине с жесткостью k = 500 Н/м. В шар попадает пуля массой m = 10 г, летящая со скоростью V = 300 м/с, и застревает в нем. Пренебрегая перемещением шара во время удара и сопротивлением воздуха, определить амплитуду А и период Т колебаний шара.

178. Однородный диск радиусом R = 30 см колеблется около горизонтальной оси, проходящей через одну из образующих цилиндрической поверхности диска. Определить приведенную длину L и период Т колебаний маятника.

179. Два одинаково направленных гармонических колебания одного периода с амплитудами А ₁ = 10 см и А ₂ = 6 см складываются в одно колебание с амплитудой А = 14 см. Найти разность фаз Δ φ складываемых колебаний.

180. Найти амплитуду А и начальную фазу φ гармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями x ₁ = 0,02×sin(5πt+π/2) м и x ₂ = 0,03×sin(5πt+π/4) м. Написать уравнение результирующего колебания, полученного от сложения этих двух колебаний.

Дата добавления: 2017-02-01