Примеры решения задач

Пример 1. Два точечных электрических заряда Q ₁ = 10 нКл и Q ₂= -20 нКл находятся в среде с диэлектрической проницаемостью ε = 2 на расстоянии d = 10 см друг от друга. Определить напряженность Е и потенциал j поля, создаваемого этими зарядами в точке А, удаленной от заряда Q ₁ на расстояние r ₁=10 см и от заряда Q ₂ на расстояние r ₂ =7 см.

Дано: Q ₁=10 нКл =10×10^-9 Кл Q ₂= -20 нКл = -20×10^-9 Кл d = 10 см = 0,1 м e = 2 r ₁ = 10 см = 0,1 м r ₂ = 7 см = 0,07 м e ₀ = 8,85×10^-12 Ф/м Е =? j =?

Решение:

Согласно принципу суперпозиции электрических полей, каждый заряд создает электрическое поле независимо от присутствия в пространстве других зарядов. Поэтому напряженность электрического поля в искомой точке может быть найдена, как геометрическая сумма напряженностей и полей, создаваемых каждым зарядом в отдельности:

.

Модули напряженности электрических полей, создаваемых точечными зарядами Q ₁ и Q ₂ в среде с диэлектрической проницаемостью e рассчитываются по формулам:

, (3.1)

(3.2)

Вектор (рис. 3.1) направлен по силовой линии от заряда Q ₁, так как этот заряд положителен; вектор направлен также по силовой линии, но к заряду Q ₂, так как этот заряд отрицателен.

Модуль вектора найдем по теореме косинусов

, (3.3)

где a -угол между векторами и в треугольнике А , который может быть найден из треугольника с известными сторонами r ₁, r ₂ и d:

.

В данном случае во избежание громоздких записей удобно значение cos a вычислить отдельно:

Подставляя выражение Е ₁ из уравнения (3.1) и Е ₂ из уравнения (3.2) в (3.3) и вынося общий множитель 1/(4 pee ₀) за знак корня, получаем

. (3.4)

В соответствии с принципом суперпозиции электрических полей потенциал j результирующего поля, создаваемого двумя зарядами Q ₁ и Q ₂, равен алгебраической сумме потенциалов

. (3.5)

Потенциал электрического поля, создаваемого точечным зарядом Q на расстоянии r от него, выражается формулой

. (3.6)

В нашем случае согласно формулам (3.5) и (3.6) получим

или .

Произведем проверку единиц измерения:

.

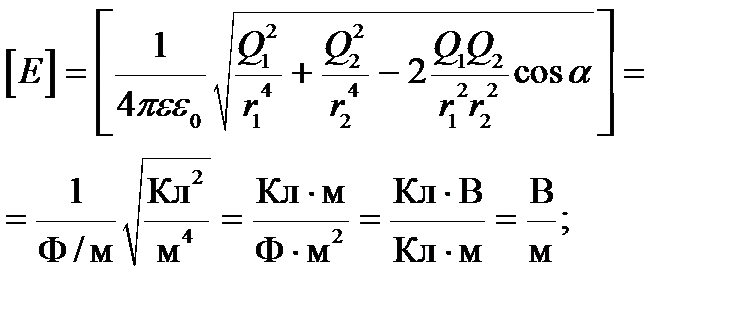
Произведем вычисления:

B/м;

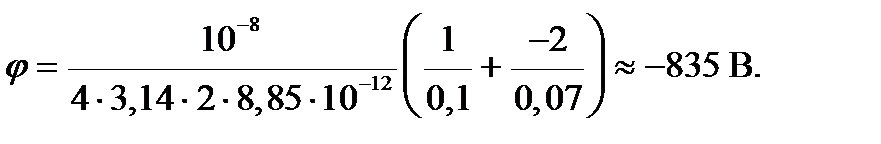
Ответ: Напряженность и потенциал в точке А соответственно равны Е = 5,6×10⁴ В/м, j = -835 В.

Пример 2. На тонком стержне длиной l = 40 см находится равномерно распределенный электрический заряд. На продолжении оси стержня на расстоянии а = 20 см от ближайшего конца находится точечный заряд Q ₁ = 4 нКл, который взаимодействует со стержнем с силой F = 10 мкН. Определить линейную плотность t заряда на стержне.

Дано: l = 40 см = 0,4 м а = 20 см = 0,2 м Q ₁= 4 нКл = 4×10^-9 Кл F = 10 мкН =10×10^-6 Н e ₀ = 8,85×10^-12 Ф/м t =?

Решение:

Выделим из стержня (рис. 3.2) малый участок dr с зарядом dQ =tdr, где t - линейная плотность заряда. Этот заряд можно рассматривать как точечный. Тогда, согласно закону Кулона для точечных зарядов в вакууме, сила взаимодействия

.

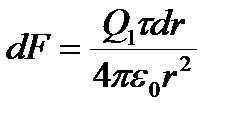Интегрируя это выражение в пределах от а до a+l получим,

.

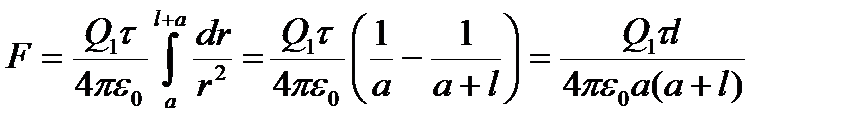Откуда

.

Произведем проверку единиц измерения:

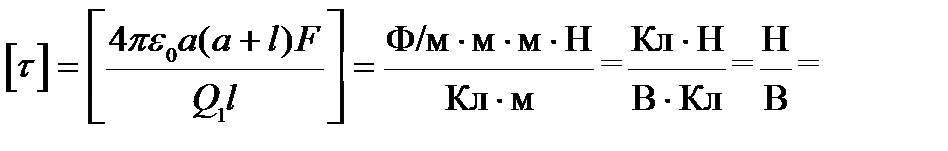
Произведем вычисления:

.

Ответ: Линейная плотность заряда на стержне t = 83,3×10^-9 Кл/м = 83,3 нКл/м.

Дано: ε = 9 q = 1×10^-9 Кл r = 1 см = 0,01 м R = 9 см = 0,09 м s = 1×10^-4 Кл/м² e ₀ = 8,85×10^-12 Ф/м А =?

Пример 3. Заряд q = 2×10^-9 Кл переносится из бесконечности в точку, находящуюся на расстоянии r = 1 см от поверхности заряженного шара радиусом R = 9 см. Поверхностная плотность положительного заряда s = 10^‑4 Кл/м². Определить совершаемую при этом работу, если диэлектрическая проницаемость среды ε = 9.

Решение:

Работа A внешней силы по перемещению заряда q из точки поля с потенциалом j ₁ в другую точку с потенциалом j ₂ равна по абсолютной величине, но противоположна по знаку работе сил поля по перемещению заряда между этими точками поля, то есть

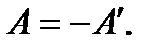
Работа сил электрического поля определяется по формуле

.

Тогда

, (3.7)

где j ₁ – потенциал в начальной точке; j ₂ – потенциал в конечной точке.

Потенциал, создаваемый заряженным шаром радиусом R в точке на расстоянии r от его поверхности, определяется по формуле

, (3.8)

где Q = 4 spR ² – заряд шара.

Потенциал j ₁ в бесконечно удаленной точке (при r ® ¥) будет равна нулю. Воспользуемся выражением (3.8) для потенциала j ₂ и подставим в формулу (3.7); после преобразований получим

.

Проверим единицы измерения:

.

Расчет:

.

Ответ: Работа перемещения заряда из бесконечности в данную точку поля равна А = 2×10^-4 Дж.

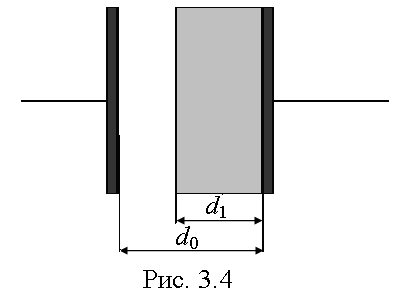
Пример 4. Между пластинами плоского конденсатора, находящимися на расстоянии d ₀ = 1 см, приложена разность потенциалов U ₁ = 200 В. К одной из пластин конденсатора прилегает плоскопараллельная стеклянная пластина (e ₁ = 7) толщиной d ₁ = 9 мм. Конденсатор отключают от источника напряжения и после этого вынимают пластину. Определить разность потенциалов между пластинами конденсатора. Во сколько раз изменится энергия конденсатора?

Дано: d ₀ = 1см = 0,01 м d ₁ = 9 мм = 9×10^-3 м U ₁ = 200 В e ₁ = 7 e ₂ = 1 U ₂ =? W ₂/ W ₁=?

Решение:

Разность потенциалов между пластинами конденсатора в случае отключения его от источника напряжения находится из условия, что заряд на его пластинах остается неизменным, то есть

, (3.9)

где С ₁ и С ₂ – емкости конденсатора; U ₁ и U ₂ – разности потенциалов.

В условиях данной задачи конденсатор вначале является слоистым и его емкость С ₁ находится по формуле, используемой для определения емкости батареи последовательно соединенных конденсаторов

, (3.10)

где S – площадь пластин; e ₁ и e ₂ – диэлектрические проницаемости стекла и воздуха; d ₁ – толщина стеклянной пластины; d ₀ – зазор между пластинами.

После удаления стеклянной пластины из зазора конденсатор становится простейшим плоским конденсатором с емкостью

. (3.11)

Разность потенциалов U ₂, которая устанавливается после удаления из зазора стеклянной пластины, определим из формулы (3.9), подставляя в нее формулы (3.10) и (3.11) и производя соответствующие преобразования:

. (3.12)

Энергия заряженного конденсатора:

.

Изменение энергии конденсатора найдем, узнав отношение энергии конденсаторов:

. (3.13)

Это отношение можно определить двумя способами:

1. Если подставить выражение для входящих в отношение (3.13) величин, то после преобразований и вычислений получим:

.

2. Отношение (3.13) можно представить в виде

.

Так как по условию С ₁ U ₁= C ₂ U ₂ (см.(3.9)), то

.

Делаем проверку единиц измерения:

.

Расчет:

Ответ: После выемки стеклянной пластины разность потенциалов между пластинами конденсатора станет равной 875 В, а энергия увеличится в 4,38 раза.

Пример 5. Определить максимальную мощность, которая может выделяться во внешней цепи, питаемой от батареи с ЭДС 12 В, если наибольшая сила тока, которую может дать батарея, равна = 5 А.

Дано: e = 12 В I _maх= 5 А Р _max =?

Решение:

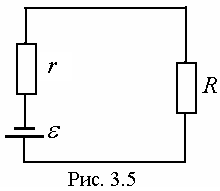
Используем Закон Ома для полной цепи:

, (3.14)

где R – сопротивление внешней цепи; r – внутреннее сопротивление источника тока.

Мощность Р, выделяемая во внешней цепи, определяется по формуле . Преобразуем это выражение, используя формулу (3.14):

. (3.15)

Таким образом, мощность зависит от внешнего сопротивления цепи R. Мощность будет максимальной при таком значении R, при котором производная dР / dR обращается в нуль.

Возьмем первую производную и приравняем к нулю:

. (3.16)

Тогда получим R = r. Определим r.

Максимальный ток возникает при коротком замыкании цепи, т.е. когда внешнее сопротивление R = 0. Исходя из этого, , откуда , значит

. (3.17)

Подставив уравнение (3.17) в уравнение (3.15) и выполнив преобразования, получим:

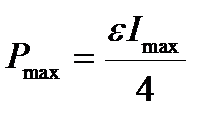. (3.18)

Проверка единиц измерения:

.

Расчет:

.

Ответ: Максимальная мощность, выделяемая во внешней цепи, равна 15 Вт.

Пример 6. Сила тока в проводнике сопротивлением R = 20 Ом нарастает в течении времени D t = 2 с по линейному закону от I ₀ = 0 до I = 6 А (рис. 3.6). Определить теплоту Q, выделившуюся в этом проводнике за вторую секунду.

Дано: R = 20 Ом D t = 2 с I ₀ = 0 I = 6 A Q =?

Решение:

Закон Джоуля – Ленца в виде справедлив для постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого интервала времени и записывается в виде

. (3.19)

Здесь сила тока I является некоторой функцией времени. В данном случае

, (3.20)

где – сила тока в начальный момент времени, k – коэффициент пропорциональности, характеризующий скорость изменения силы тока. Как видно из рис. 3.6

.

С учетом формулы (3.20) формула (3.19) примет вид

. (3.21)

Для определения теплоты, выделившейся за конечный интервал времени D t, выражение (3.21) надо проинтегрировать в пределах от t ₁ до t ₂:

.

Проверка единиц измерения:

.

Расчет:

Дж.

Ответ: За вторую секунду в проводнике выделится 420 Дж теплоты.

Дата добавления: 2017-02-01