Примеры решения задач

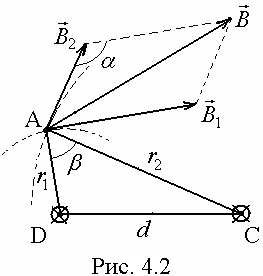Пример 1. Два параллельных бесконечно длинных провода D и С, по которым текут в одном направлении одинаковые токи (I = 60 А), расположены на расстоянии d = 10 см друг от друга. Определить индукцию магнитного поля, создаваемого проводниками с током в точке А (рис. 4.2), отстоящей от оси одного проводника на расстоянии r ₁ = 5 см, от другого на расстоянии r ₂ = 12 см.

Дано:

I₁ =I₂ = I = 60 А

d = 10 cм = 0,1 м

r ₁ = 5 см = 0,05 м

r ₂ = 12 см = 0,12 м

m ₀ = 4 p ×10^-7 Гн/м

В =?

Решение:

Для нахождения индукции 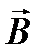результирующего магнитного поля в точке А, воспользуемся принципом суперпозиции магнитных полей:

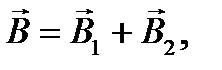
где 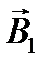- вектор индукции магнитного поля, создаваемого проводом D на расстоянии r ₁ в точке А; - вектор индукции магнитного поля, создаваемого проводом С на расстоянии r ₂ в точке А.

Провода D и С, по которым текут токи в одном направлении (обозначение Ä или Å - токи текут от нас), расположены перпендикулярно рисунку и видны только их сечения.

Направления векторов 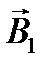и определим с помощью правила правого винта. Если вдоль тока I ₁ расположить винт и вращать его по часовой стрелке, то он будет удаляться от нас. Вектор 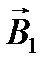направлен по касательной, проведенной через точку А на окружности радиуса r ₁, в сторону вращения (пунктирная линия – часть этой окружности). Аналогично определяем направление вектора .

Модуль вектора 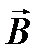найдем, используя теорему косинусов:

, (4.1)

где a - угол между векторам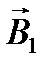и и 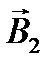в треугольнике А .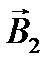

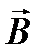Из рис. 4.2 видно, что

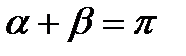Þ 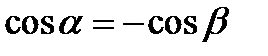. (4.2)

Применив теорему косинусов к треугольнику с известными сторонами r ₁, r ₂ и d, найдем

.

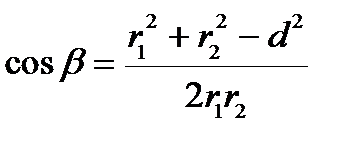Во избежание громоздких записей удобно значение cos b вычислить отдельно:

.

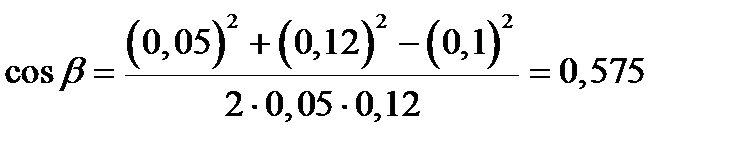Таким образом, учитывая (4.2), cos a = - 0,575.

Индукци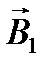и и 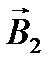магнитных полей, создаваемых прямыми токами I ₁ и I ₂, определяются по формулам:

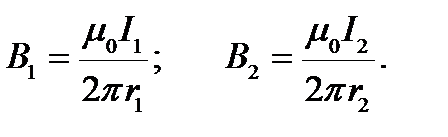
Учитывая, что I ₁ = I ₂ = I, подставим выражения В ₁ и В ₂ в формулу (4.1), и вынесем за знак корня общие члены:

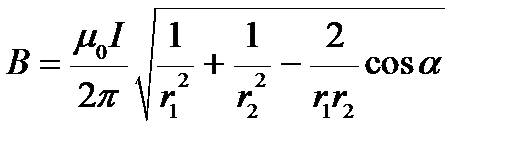. (4.3)

Проверим единицы измерения:

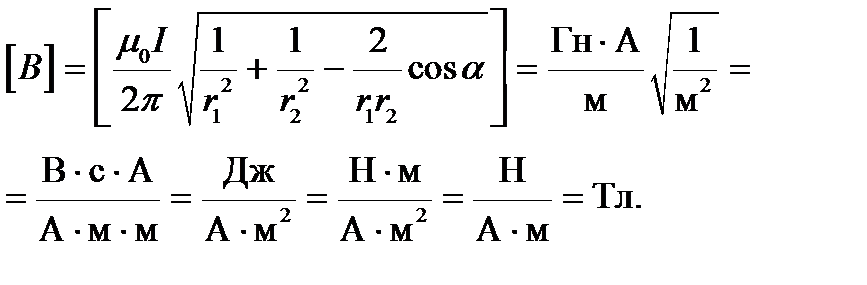
Подставим в формулу (4.3) числовые значения физических величин и произведем вычисления:

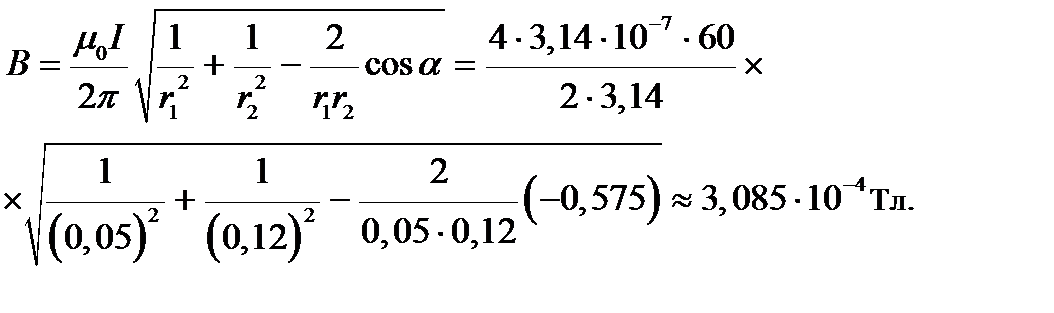
Ответ: Индукция результирующего магнитного поля в точке А, создаваемого проводами с токами, В = 3,085×10^-4 Тл.

Дано: l ₁ = l ₂ = l= 2,5 м d = 20 см = 0,2 м I = 1 кА =10³ А F =?

Пример 2. По двум прямым параллельным проводам длиной l = 2,5 м каждый, находящимся на расстоянии d = 20 см друг от друга, текут одинаковые токи I = 1 кА. Вычислить силу взаимодействия токов.

Решение:

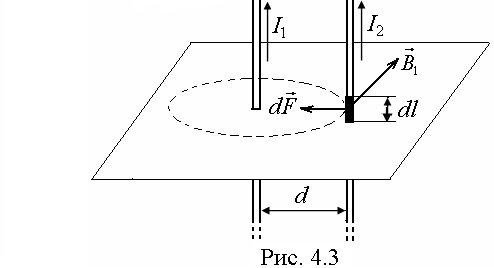
Взаимодействие двух проводов, по которым текут токи, осуществляется через магнитное поле. Каждый ток создает магнитное поле, которое действует на другой провод.

Предположим, что оба тока (обозначим их для удобства I ₁ и I ₂) текут в одном направлении. Ток I ₁ создает в месте расположения второго провода (с током I ₂) магнитное поле.

Направление вектора индукции магнитного поля в данной точке пространства определяется по правилу правого винта. Для этого проведем линию магнитной индукции вокруг первого тока радиуса d (пунктир на рис. 4.3) и по касательной к ней в сторону вращения винта (направления тока I ₁) – вектор магнитной индукции 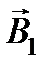. Модуль магнитной индукции В ₁, создаваемой прямым бесконечно длинным проводом с током I ₁ в вакууме (m = 1) на расстоянии d от его оси, определяется соотношением

. (4.4)

Согласно закону Ампера, на каждый элемент второго провода с током I ₂длиной dl действует в магнитном поле сила

,

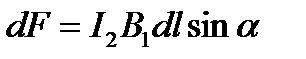где a – угол между векторам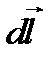и и 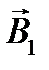. Так как вектор 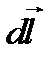перпендикулярен вектору 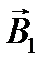, то sin a =1 и, тогда

.

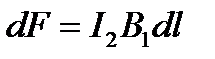Подставив в это выражение В ₁, согласно соотношению (4.4), получим

.

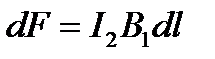Направление силы определяется правилом левой руки. Силу взаимодействия проводов с током найдем интегрированием

.

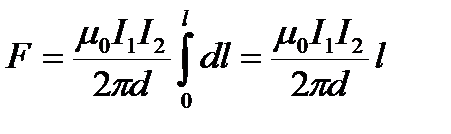Согласно условию задачи I ₁ = I ₂= I, тогда получим:

.

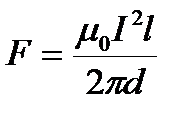Проверим размерность полученной формулы:

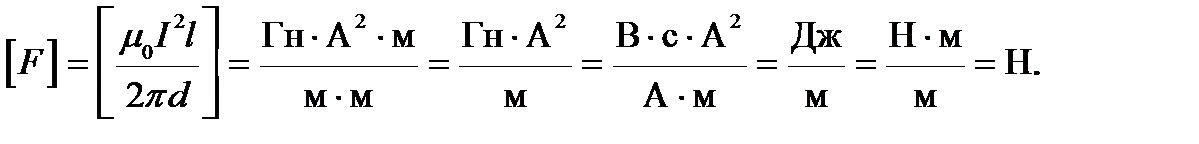
Расчет:

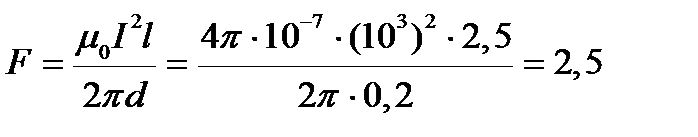Н.

Ответ: Сила взаимодействия токов F = 2,5 Н.

Пример 3. Протон, прошедший ускоряющую разность потенциалов U = 600 В, влетел в однородное магнитное поле с индукцией В = 0,3 Тл и начал двигаться по окружности. Вычислить радиус R окружности.

Дано: U = 600 В q = 1,6×10^-19 Кл m = 1,67×10^-27 кг В = 0,3 Тл R =?

Решение:

Движение заряженной частицы в однородном магнитном поле будет происходить по окружности только в том случае, когда частица влетит в магнитное поле перпендикулярно линиям магнитной индукции 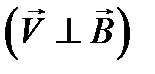. Так как сила Лоренца 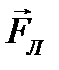перпендикулярна вектору скорости 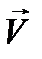, то она сообщит частице (протону) нормальное ускорение .

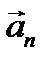Согласно второму закону Ньютона:

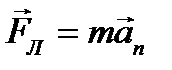, (4.5)

где m – масса протона.

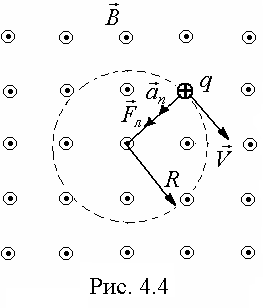
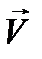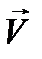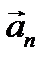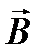На рис. 4.4 совмещена траектория протона, имеющего положительный заряд q, с плоскостью чертежа и дано (произвольно) направление вектора . Силу Лоренца направим перпендикулярно вектору к центру окружности (векторы и сонаправлены). Используя правило левой руки, определим направление магнитных силовых линий ( -вектор перпендикулярен плоскости рисунка и направлен на нас).

Перепишем выражение (4.5) в скалярной форме (в проекции на радиус):

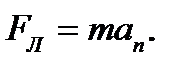(4.6)

В скалярной форме 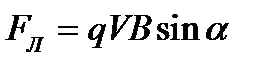. В нашем случае 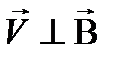и sina = 1, тогда 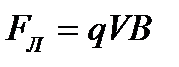. Так как нормальное ускорение 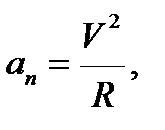то выражение (4.6) перепишем следующим образом:

Отсюда находим радиус окружности:

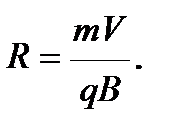
Заметив, что mV есть импульс протона (р), это выражение можно записать в виде

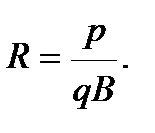(4.7)

Импульс протона найдем, воспользовавшись связью между работой сил электрического поля и изменением кинетической энергии протона, т.е.

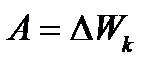или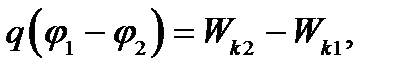

где 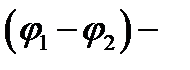ускоряющая разность потенциалов (или ускоряющее напряжение U); 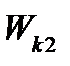и 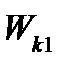– конечная и начальная кинетические энергии протона.Пренебрегая начальной кинетической энергией протона 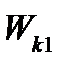и выразив кинетическую энергию 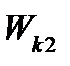через импульс р, получим:

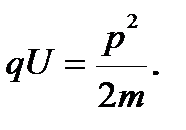
Найдем из этого выражения импульс 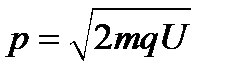и подставим его в формулу (4.7):

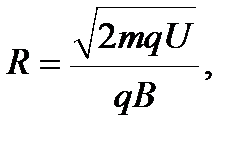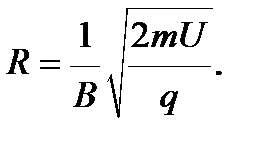или (4.8)

Сделаем проверку единиц измерения:

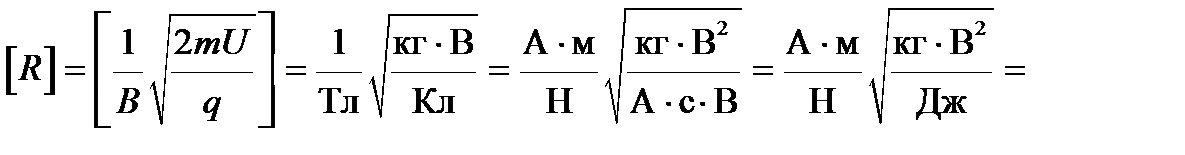
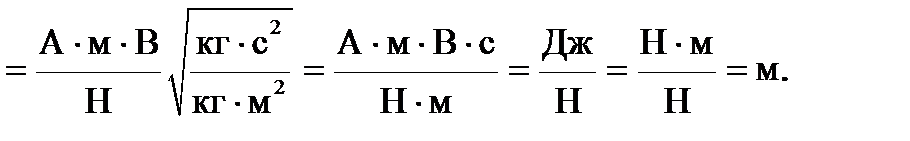
Расчет:

Ответ: Радиус окружности, по которой движется протон, R = 1,18 см.

Пример 4. Плоский квадратный контур со стороной а = 10 см, по которому течет ток I = 100 А, свободно установился в однородном магнитном поле (В ₁ = 1 Тл). Определить работу А, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон на угол: 1) j ₁ = 90^о; 2) j ₂ = 3^о. При повороте контура сила тока в нем поддерживается неизменной.

Дано: а = 10 см = 0,1 м I= 100 A = const B = 1 Тл j ₁ = 90^о j ₂ = 3^о А ₁ =? А ₂ =?

Решение:

На контур с током в магнитном поле действует момент силы (рис. 4.5)

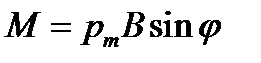, (4.9)

где p_m=IS =Ia ² – магнитный момент контура; В – магнитная индукция; j – угол между векторами 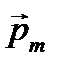(направлен по нормали к контуру) и .

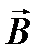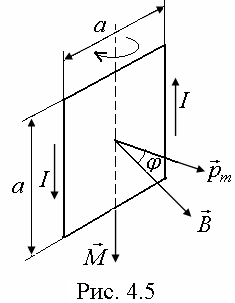По условию задачи в начальном положении контур свободно установился в магнитном поле. При этом момент силы равен нулю (М = 0), а значит, j = 0, то есть векторы 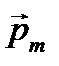и 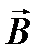сонаправлены. Если внешние силы выведут контур из положения равновесия, то возникший момент сил 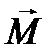будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил 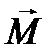переменный (зависит от угла поворота j), то для подсчета работы применим формулу работы в дифференциальной форме dA=Mdj. Учитывая формулу (4.9), получим

.

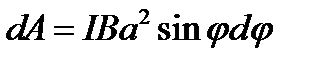Взяв интеграл от этого выражения, найдем работу при повороте на конечный угол

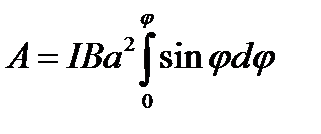. (4.10)

Работу при повороте на угол j ₁ = 90^о определим по формуле

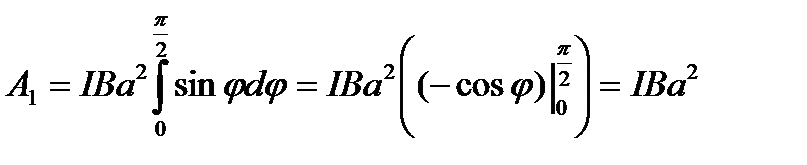. (4.11)

Чтобы рассчитать работу внешних сил при повороте на угол j ₂ = 3^о, учтем, что угол j ₂ мал, и заменим в выражении (4.10) sin j на j (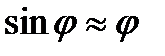), выраженному в радианах:

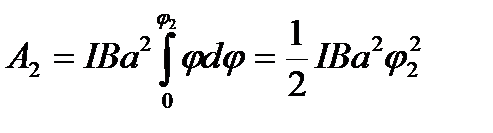. (4.12)

Сделаем проверку единиц измерения:

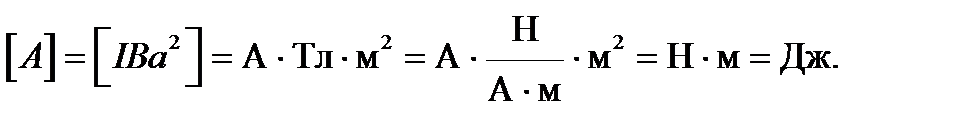
Расчет:

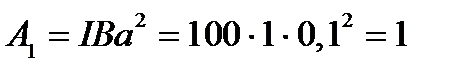Дж;

.

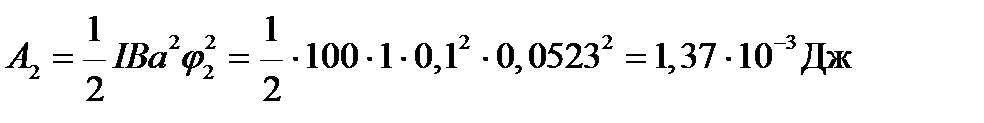Задачу можно решить и другим способом.

Работа внешних сил по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, пронизывающего контур:

,

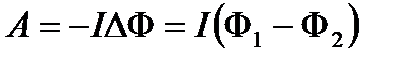где Ф₁ – магнитный поток, пронизывающий контур до перемещения; Ф₂ – то же, после перемещения.

Если j ₁ = 90^о, то Ф₁= BS, Ф₂ = 0. Следовательно,

,

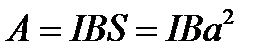что совпадает с уравнением (4.11).

Ответ: Работа, совершаемая внешними силами, по повороту рамки на угол 90^о равна 1 Дж, а на 3^о – 1,37×10^-3 Дж.

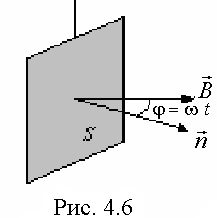Пример 5. В однородном магнитном поле (В = 0,1 Тл) равномерно с частотой п = 10 с^-1 вращается рамка, содержащая N = 1000 витков, плотно прилегающих друг к другу. Площадь рамки S = 150 см². Определить мгновенное значение ЭДС индукции, соответствующее углу j поворота рамки, равному 30^о.

Дано: В = 0,1Тл п = 10 с^-1 j = 30^о N = 1000 S = 150 см² = 0,015 м² e =?

Решение:

Мгновенное значение ЭДС индукции e определяется основным уравнением электромагнитной индукции Фарадея – Максвелла:

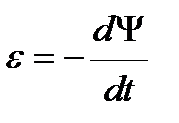, (4.13)

где Y – потокосцепление.

Потокосцепление Y связано с магнитным потоком F и числом N витков, плотно прилегающих друг к другу, соотношением

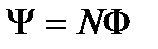. (4.14)

Подставляя выражение Y в формулу (4.13), получаем

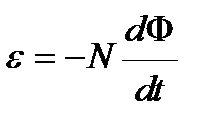. (4.15)

При вращении рамки магнитный поток F, пронизывающий рамку в момент времени t, определяется соотношением

,

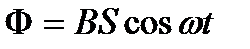где В – магнитная индукция; S – площадь рамки; w – круговая (или циклическая) частота.

Подставив в формулу (4.15) выражение F и продифференцировав полученное выражение по времени, найдем мгновенное значение ЭДС индукции

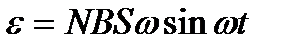. (4.16)

Круговая частота w связана с частотой вращения п соотношением

. (4.17)

Подставляя выражение (4.17) в формулу (4.16) и заменив wt на j, получим:

.

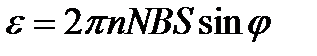Проверим единицы измерения:

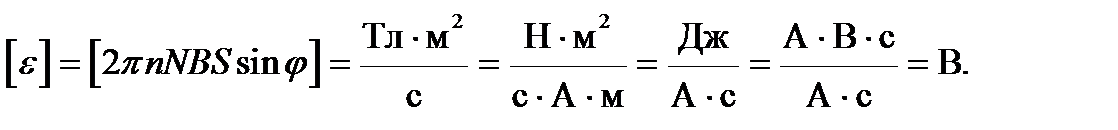
Расчет:

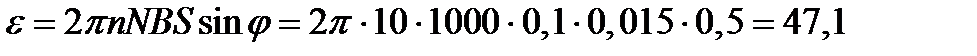В.

Ответ: При повороте рамки на угол j = 30^о к силовым линиям однородного магнитного поля, возникающая в ней ЭДС индукции, будет равна e = 47,1 В.

Пример 6. Соленоид, сопротивление которого R = 2 Ом, подключается к аккумулятору с ЭДС e = 8 В. Спустя время t = 0,01 с, сила тока в цепи достигает значения I = 1 А. Определить коэффициент самоиндукции соленоида, если сопротивление аккумулятора ничтожно мало.

Дано: R = 2 Ом e = 8 В t = 0,01 с I = 1 А; r = 0 L =?

Решение:

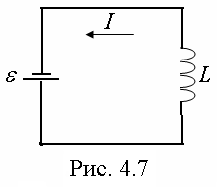Зависимость силы тока от времени, прошедшего с момента замыкания соленоида, определяется соотношением

.

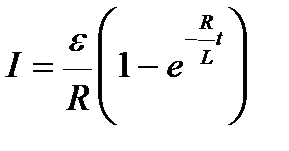Откуда находим

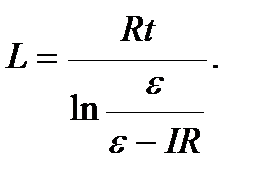
Проверим единицы измерения:

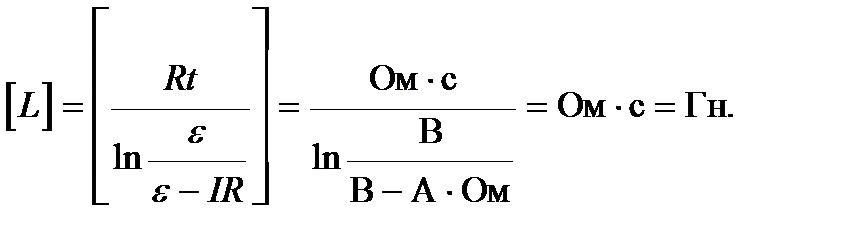
Расчет:

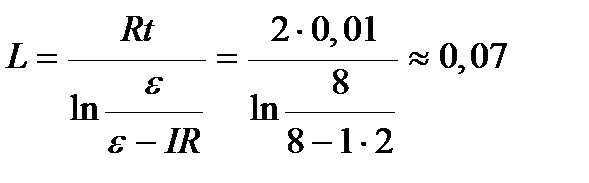Гн.

Ответ: Индуктивность соленоида L = 0,07 Гн.

Пример 7. Соленоид с сердечником из немагнитного материала содержит N = 1200 витков провода, плотно прилегающих друг к другу. При силе тока I = 4 А магнитный поток F = 6 мкВб. Определить индуктивность L соленоида и энергию W магнитного поля соленоида.

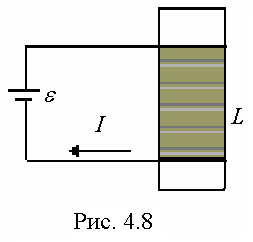
Дано: N = 1200 I = 4 A F = 6 мкВб = 6×10^-6 Вб L =? W =?

Решение:

Индуктивность L связана с потокосцеплением Y и силой тока I соотношением

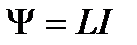. (4.18)

Потокосцепление, в свою очередь, может быть определено через поток F и число витков N (при условии, что витки плотно прилегают друг к другу)

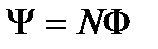. (4.19)

Из формул (4.18) и (4.19) находим индуктивность соленоида

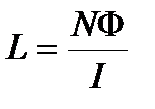. (4.20)

Энергия магнитного поля соленоида

.

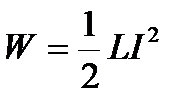Выразим L согласно (4.20), получим:

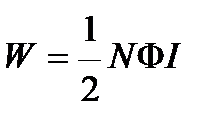. (4.21)

Проверим единицы измерения:

;

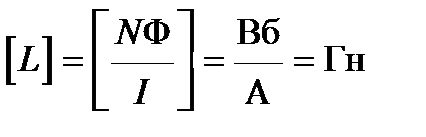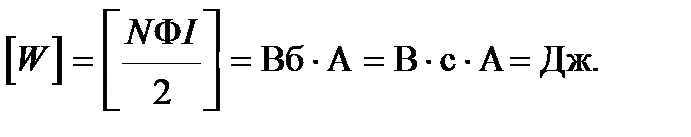
Подставив в формулы (4.20) и (4.21) значения физических величин, произведем вычисления:

;

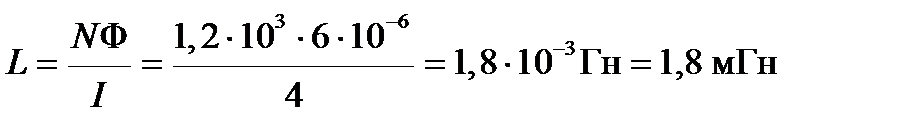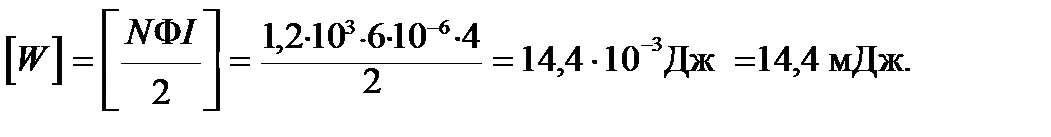
Ответ: Индуктивность соленоида L = 1,8 мГн; энергия магнитного поля в нем W = 14,4 мДж.

Дата добавления: 2017-02-01