При решении задач без вывода

Перечень формул, которые можно использовать

Количество вещества – число структурных элементов (молекул, атомов и т.д.), содержащихся в теле (системе)

,

где N – число структурных элементов, N_А – число Авогадро.

Молярная масса вещества:

,

где m – масса тела.

Концентрация молекул

,

где V – объем тела.

Уравнение состояния идеального газа

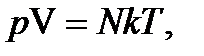
где р – давление газа, V – его объем, N – количество молекул газав данном объеме, Т - термодинамическая температура, выраженная в кельвинах, k – постоянная Больцмана.

Уравнение Менделеева-Клапейрона

,

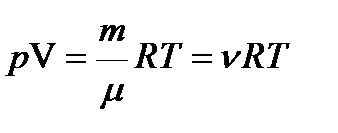где R = 8,31 - универсальная газовая постоянная.

Опытные газовые законы для двух состояний идеального газа:

1. Закон Бойля-Мариотта (изотермический процесс: Т = const, m = const):

.

2. Закон Гей-Люссака (изобарный процесс: р = const, m = const):

.

3. Закон Шарля (изохорный процесс: V= const, m = const):

.

4. Объединенный газовый закон (m = const):

.

Закон Дальтона:

,

где р – давление смеси газов; р ₁, р ₂, …, р _n – парциальные давления – давления каждой из компонентов смеси.

Основное уравнение молекулярно-кинетической теории газа (уравнение, задающее связь между макро - и микропараметрами):

,

где р – давление газа; п – концентрация молекул газа (число молекул в единице объема); <e_n> - средняя кинетическая энергия поступательного движения молекулы.

Средняя кинетическая энергия молекулы или полная энергия молекулы, приходящаяся на все степени свободы:

,

где i – число степеней свободы молекулы.

Зависимость давления газа от концентрации молекул

.

Скорости молекул:

а) средняя квадратичная

,

б) средняя арифметическая

,

в) наиболее вероятная

,

где т ₀ – масса одной молекулы; R – универсальная газовая постоянная; m - молярная масса газа, k – постоянная Больцмана, Т – термодинамическая температура.

Средняя длина свободного пробега молекул газа

,

где n – концентрация молекул, d – эффективный диаметр молекул газа.

Среднее число соударений, испытываемых одной молекулой газа в единицу времени

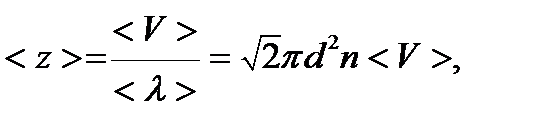
где - средняя арифметическая скорость молекул.

Связь между удельной с и молярной С теплоемкостями газа

.

Молярная теплоемкость газа при постоянном давлении С_р и постоянном объеме С _V

,

где i – число степеней свободы молекул идеального газа, R - универсальная газовая постоянная.

Уравнение Майера

.

Первое начало термодинамики

,

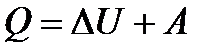где Q – количество теплоты, сообщаемое системе, D U – изменение внутренней энергии системы, А – работа, совершаемая системой (идеальным газом) против внешних сил.

При бесконечно малом сообщении теплоты

,

где dU – бесконечно малое изменение внутренней энергии системы, dA - элементарная работа, совершаемая газом.

Изменение внутренней энергии идеального газа

,

где i – число степеней свободы молекул; 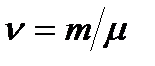- количество вещества.

Работа при изменении объема газа в общем случае вычисляется по формуле

где V₁ – начальный объем газа, V₂ – его конечный объем.

Работа газа:

а) при изохорном процессе (V = const, m = const)

,

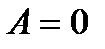б) при изобарном процессе (р = const, m = const)

,

в) при изотермическом процессе (Т = const, m = const)

,

г) при адиабатном процессе (dQ = 0)

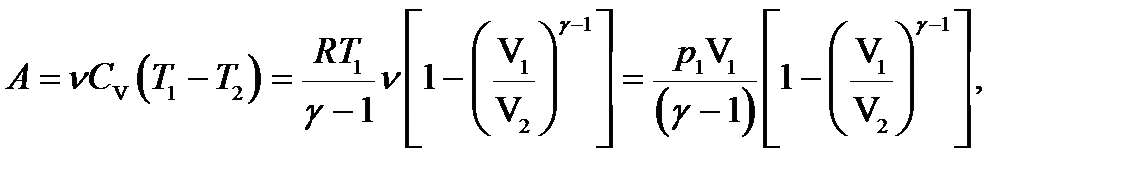
где – показатель адиабаты.

Уравнения адиабатного процесса для двух состояний идеального газа (уравнения Пуассона):

КПД цикла любой тепловой машины

,

где A – работа, совершаемая газом за цикл, Q ₁ – количество теплоты, получаемое рабочим телом (газом) за цикл от нагревателя, Q ₂ – количество теплоты, отдаваемое за один цикл холодильнику.

Термический коэффициент полезного действия цикла Карно:

,

где Т ₁ и Т ₂ – соответственно абсолютные температуры нагревателя и холодильника.

Дата добавления: 2017-02-01