Образование скачков уплотнения

Волна В К называется плоским косым скачком уплотнения или плоской ударной волной. При переходе через такую ударную волну поток испытывает скачкообразные изменения давления, скорости и других параметров. Положение скачка определяется углом р между плоскостью скачка ВК и первоначальным направлением потока АВ.

Образование косых скачков уплотнения можно просле­дить также на простейшем примере обтекания стенки ABC, повернутой в точке В на некоторый конечный угол 6 на­встречу потоку.

Благодаря такому повороту стенки сечение струйки уменьшается и она суживается. В сверхзвуковом потоке это приведет к повышению давления (р₂> р1). Причем повышение давления происходит скачкообразно при пере­ходе через поверхность В К, являющуюся поверхностью скачка. Можно показать, что при обтекании рассматривае­мой Стенки непрерывный переход от параметров в области АВК к параметрам в области КВС физически невозможен.

Действительно, границей возмущения для области АВК_г должна быть звуковая волна ВК, угол наклона которойк вектору скорости с_х будет 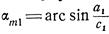. Вторая граница возмущения ВК₂ имеет угол наклона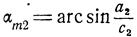

Так как 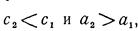то 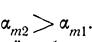Характеристика ВК₂ оказывается в невозмущенной области АВК_г и линии тока должны были бы иметь форму, показанную пункти­ром, что физически совершенно нереально.

Можно предположить, что косой скачок занимает сред­нее положение между волнами ВК_Х и ВК₂\ тогда угол косого скачка (3 связан простым приближенным соотноше­нием с углами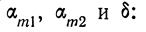

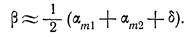
Такой случай соответствует набеганию плоского сверхзвукового потока постоянной скорости на бесконечный клин или движению пло­ского клина в среде с постоянной сверхзвуковой скоростью. При не­стационарном движении скачки уплотнения могут возникать и при дозвуковых скоростях движения. В общем случае нестационарного движения ударная волна, являющаяся результатом конечного уплотне­ния или разрежения потока, может перем-ся относ-но твер­дого тела, которое вызвало ударную волну.

21. Уравнения косого скачка

Рассматр-м установившееся течение газа без теплообмена с окружающей средой и без трения. Предположим, что в некоторой точке сверхзвукового потока возник косой скачок уплотнения. Параметры газа до скачка обозначены индексом 1, а за скачком — соответственно индексом 2.

Рассмотрим движение газа по линии тока АВС, пересекающей плоскость косого скачка в точке В. Как указывалось, при переходе через косой скачок линия тока деформируется, отклоняясь на некоторый угол б. Скорость до и после косого скачка можно представить составляющими, нормальными к плоскости скачка (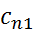 и 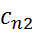) и касательными к ней и, таким образом, построить треугольники скоростей до и после скачка.

Очевидно, что

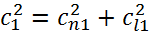
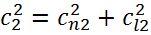
Для решения основной задачи о косом скачке, которая сводится к установлению связи между параметрами до и после скачка и к определению потерь, возникающих при переходе через скачок, используем основные законы механики.

Закон сохранения массы—уравнение неразрывности-для двух сечений трубки тока до и после скачка может быть записано в следующем виде:

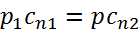
Закон сохранения импульсов –уравнение изменения количества движения—в проекции на нормаль к плоскости косого скачка дает

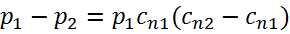
Или

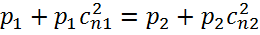
В Проекции на плоскость скачка получим

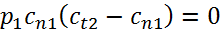
22. Ударная поляра

Зависимость между параметрами на скачке можно в весьма удобной форме представить графически. С этой целью рассмотрим треугольники скоростей на скачке (рис. 4-7).

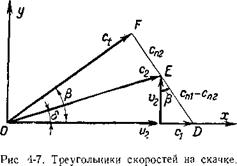Расположим вектор скорости до скачка с_х по оси х (отрезок OD). Отрезки OF и FD представляют собой соот­ветственно касательную c_t и нормальную с_пХ составляю­щие скорости до скачка. Зная угол отклонения потока 8,

проведем линию вектора скорости за скачком с₂ до пере­сечения с отрезком FD. Точка пересечения (точка Е) опре­деляет величину вектора с₂, а отрезок EF выражает нор­мальную составляющую скорости за скачком.

Вектор скорости с₂ можно представить двумя другими составляющими: и₂ и v₂. Компоненты и₂ и v₂ являются про­екциями с₂ на направление скорости потока перед, скачком и на нормаль к этому направлению.

Найдем уравнение кривой, описываемой концом вектора скорости за скачком с₂, при постоянном значении вектора скорости перед скачком с_х и переменных значениях угла поворота потока за скачком 6.

Выражая это уравнение в форме связи между и₂ и и_2У мы получим кривую скорости за скачком в плоскости го­дографа скорости.

Кривая, отвечающая уравнению называется ударной полярой. Кривая при надлежит к классу гнпоцнссоид. Ударная поляра может быть широко использована для расчета косых скачков графоаналитическим методом и для выяснения некоторых особенностей таких скачков.

Дата добавления: 2017-02-01