Учет влияния сжим-сти по методу малых возмущений

Рассматриваемый метод оценки влияния сжимаемости в плоском дозвуковом течении применим в тех случаях, когда возмущение потока можно считать слабым.

Излагаемый метод, предложенный Л. Прандтлем, основывается на предположении, что отклонение скорости возмущенного течения от скорости невозмущенного потока с_оо = u_оо настолько мало, что степенями указанного отклонения выше первой можно пренебречь. Уравнение для потенциала скорости является линейным дифференциальным уравнением, поэтому метод малых возмущений вызывается также методом линеаризации. Рассматриваемый метод может дать удовлетворительные результаты при расчете обтекания тонких слабо изогнутых профилей, расположенных под небольшими углами к направлению скорости невозмущенного течения, а также при исследовании потока в каналах с малой кривизной ограничивающих стенок. Вблизи точек разветвления потока (критические точки на поверхности обтекаемого тела) основное допущение метода не оправдывается, так как в этих областях поток тормозится и величина изменения скорости соизмерима со скоростью на бесконечности. Из Формул следует, что при обтекании одного и того же тела газом скорость и разность давле­ний больше, чем в случае обтекания несжимаемой жидко­стью.

Влияние сжимаемости сказывается в том, что в области положи­тельных значений р коэффи­циенты давления для сжимае­мой жидкости будут выше, а в области отрицательных значений—ниже, чем для не­сжимаемой жидкости. Следо­вательно, благодаря сжимае­мости увеличиваются абсолютные значения коэф-та давления. При этом области мин-ных давлений становятся более крутыми и вытя­гиваются. с ростом М увеличивается S, заключенная между кривыми давлений для верхней и нижней поверх-ей профиля. При этом, очевидно, подъемная сила с увел-ем возрастает.

15. Теорема Н. Е. Жуковского

Теория силового воздействия потока идеального жидкости на обтекаемые тела основывается на известной теореме Н.Е. Жуковского. Н.Е. Жуковский установил вихревое происхождение силы взаимодействия и нашел простую связь между этой силой интенсивностью циркуляционного течения, возникающего при обтекании тела. Для доказательства теоремы Жуковского воспользуемся схемой.

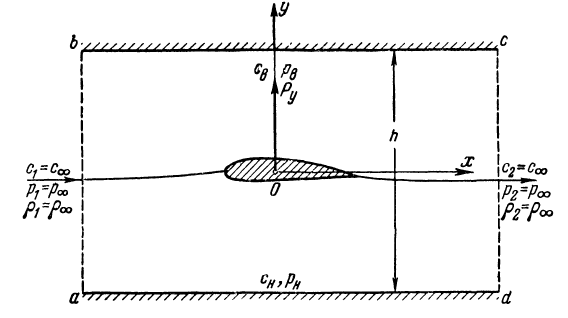
Формула выражает теорему Н.Е. Жуковского.

Теорему Жуковского можно сформулировать так: при обтекании тела плоскопараллельным безграничным потоком идеальной сжимаемой жидкости на тело единичного размаха действует сила, равная произведению циркуляции скорости Г на скорость С∞ и на плотность P∞ невозмущенного потока. Направление этой силы нормально к направлению скорости невозмущенного потока С∞. При этом, как следует из вывода, если цирку­ляция скорости, вычисленная при обходе по часовой стрел­ке, окажется положительной, то и Р_y будет положитель­ной. Подъемную силу Р_y часто называют силой Жуковского.

Дата добавления: 2017-02-01