Осн-е уравн-я одномерного теч-я. Скорость звука

Уравн-я движ-я в гидромех-ой ф-ме. Уравн-я Громеко

Уравнения Громеки – попросту другая, несколько преобразованная форма записи уравнения Эйлера.

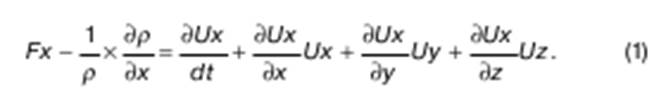Например, для координаты x Чтобы его преобразовать, используют уравнения компонентов угловой скорости для вихревого движения.

Преобразовав точно так же y-вую и z-вую компоненту, окончательно приходим к форме Громеко уравнения Эйлера

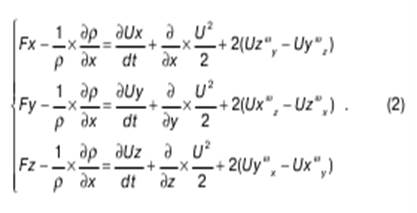Уравнение Эйлера было получено российским ученым Л. Эйлером в 1755 г., и преобразовано в вид (2) опять же российским ученым И. С. Громекой в 1881 г

Уравнение Громеко (под воздействием массовых сил на жидкость):

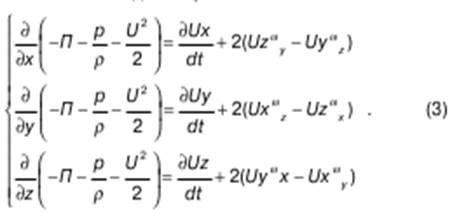
Поскольку

– dП = Fxdx + Fydy + Fzdz, (4)

то для компонентов Fy, Fz можно вывести те же выражения, что и для Fx, и, подставив это в (2), прийти к (3).

Уравнения газодинамики явл-ся матем-им выражением трех основных законов природы — законов сохранения массы, энергии и импульса.

Уравнение неразрывности. Закон сохранения массы выражается уравнением неразрывности, которое имеет вид ,

где G — массовый секундный расход газа, кг/с; 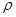— плотность газа, кг/м³, с — скорость газа, м/с; F— площадь поперечного се­чения струйки, м².

Это уравнение свидетельствует о постоянстве массового секундного расхода газа по длине струйки.

Уравнение энергии. Уравнением энергии выражается закон сохранения и превращения энергии, в соответствии с которым теплота, подведенная к единице массы газа, идет на увеличение его внутренней и кинетической энергии, на работу перемещения газа вдоль струйки и на совершение им механической работы.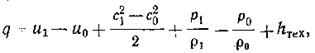

где q — подведенная извне теплота; (U₁—U₀) — приращение внутренней, а 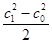— приращение кинетической энергии газа; 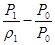— работа перемещения газа от одного сечения до другог сечения, совершаемая против сил давления; h_тех — совершаемая газом техническая работа, например вращение колеса турбины. Все величины выражаютсяжаются в джоулях на килограмм (Дж/кг). Следует отметить, что приведенное уравнение справедливо как для невязкого, так и для вязкого газа.

Обобщенное уравнение Бернулли. Урав-ие, выраж-е закон сохранения импульса, в дифференциальной форме может быть записано в виде

Если тех-ая работа не совер-ся, то ур-ие принимает вид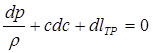

Для невязкого газа из уравнения следует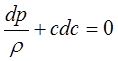

Скорость звука — скорость распространения упругих волн в среде: как продольных, так и поперечных, сдвиговых. Опр-ся упругостью и плотностью среды: как правило, в газах скорость звука меньше, чем в жидкостях, а в жидкостях — меньше, чем в твёрдых телах.

Скорость звука в газах описывается следующей формулой:

7. Различные формы уравнения энергии

Приращение любого вида энергии равно разности количеств этого вида энергии в положениях 1’ — 2' и 1 — 2. Ввиду того, что заштрихованный объем 1’ — 2 является общим для этих двух положений, приращение энергии измеряется разностью количеств энергии в бесконечно малых объемах 2 — 2' и. 1 — 1'. Отсюда следует, что приращение кинетической энергии равно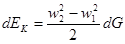

На основания выделенной части струйки газа действуют на­правленные внутрь и по нормали к ним внешние силы давления р. При перемещении газа внешние силы давления произво­дят работу. Например, перенос газа из сечения 1 в сечение 1’ происходит как бы под действием поршня площадью F₁ с дав­лением р₁. Работа поршня за время dτ равна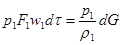

Точно так же можно представить себе, что давление р₂ на сече­ние 2 осуществляется поршнем площадью F_2. За время dτ газ переместит поршень в положение 2, производя отрицательную работу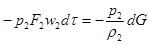

Силы давления, действ-е на боковую поверхность струй­ки (поверхность тока), никакой работы не производят, так как они нормальны к траекториям движения частиц газа. Таким об­разом, энергия, внесенная силами давления, равна разности между работами поршня 1 и поршня 2: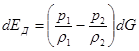

К газовой струйке на участке 1 — 2 может быть за время dt подведено тепло в количестве 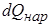. Далее газовая струйка за время dτ может произвести техническую работу dl, например, приводя во вращение колесо турбины, установленное между се­чениями 1 и 2. Наконец, следует учесть энергию, расходуемую газом за время dτ на преодоление сил трения dl_Tp.

Согласно первому началу термодинамики подведенные к газу тепловая энергия и работа сил давления расходуются на совершение технической работы, работы сил трения, а также на изменение внутренней энергии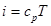

Используя выражения, можно придать урав­нению энергии следующую форму: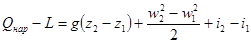

Уравнение энергии иногда называют также уравнением теплосодержания. Существенно то обстоятельство, что уравнение теплосодержания не содержит работы трения.

Дата добавления: 2017-02-01