Потери в скачках уплотнения

Изменение энтропии в скачке

При переходе через скачок уплотнения энтропия газа возрастает.

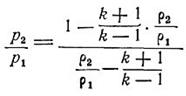Увеличение энтропии при переходе через скачок объясняется необратимым характером изменения состояния газа в скачке, «ударным» характером процесса. В результате такого процесса часть кинетической энергии газа необратимо переходит в тепло; при отсутствии энергетического обмена с внешней средой внутренняя энергия потока необратимо возрастает. Кривую, характеризующую процесс, протекающий по уравнению (4-28), называют ударной адиабатой

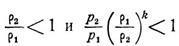Для скачка разрежения получаем

Δs<0, что невозможно при отсутствии энергетического обмена с внешней средой, так как противоречит второму закону термодинамики. Отсюда следует, что скачки разрежения в энергетически изолированном течении не могут возникнуть, так как это противоречило бы второму началу термодинамики. Однако, в сверхзвуковом течении волна разрежения с непрерывным падением давления представляет собой вполне устойчивое явление; энтропия при переходе через такую волну сохраняется неизменной

Рассмотрим более подробно энергетические преобразо­вания в скачках. Предполагая энергетически изолированное течение, заключаем, что полная энергия потока при пере­ходе через скачок не меняется. Это значит, что

или, пользуясь параметрами полного торможения,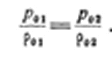

Условие можно заменить эквивалентным условием постоянства энтальпии торможения при переходе через скачок: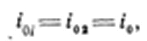

или при

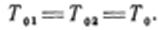
Имея в виду эти условия, рассмотрим процесс скачка в диаграмме is. Зная давление торможения до скачка p_tl и энтальпию торможения /_#, найдем в диаграм­ме is точку О,, характеризующую состояние иэоэнтропи- чески заторможенного газа до скачка. По известной ско­рости потока до скачка с, или давлению р_х находим точку D, которая определяет состояние движущегося газа перед скачком. В скачке статическое давление потока уве­личивается до р,. Если известен угол отклонения потока I и, следовательно, (3, то состояние газа за скачком опреде­лено, так как по формуле можно найти приращение энтропии &s*. Заметим, что ли­ния, соединяющая точки D и F._t на рис. 4-11, не характе­ризует изменения состояния газа в скачке, так как в диаграмме из неквазистатнческие процессы могут быть представ­лены тольео начальной и конечной точками процесса.

Если поток за скачком кэоэнтропически затормозить, то состояние латного торможения характеризуется точкой 0„ в которой легко находится значение. Если предоставить теперь потоку возможность нзоэнтролически расшириться до давления перед скачком, то его состояние будет опре­делено точкой Е. Скорость газа при этом может быть вычислена по уравнению энергии:

25. Постр-ие проц-са в диагр-е i-s диагр-е. Скачки уплотн-я в реал-ом газе

рассмотрим процесс скачка в диаграмме is. Зная давление торможения до скачка р01 и энтальпию торможения, найдем в диаграмме is точку характеризующую состояние изоэнтропически заторможенного газа до скачка. По известной скорости потока до скачка г или давлению, находим точку, которая определяет состояние движущегося газа перед скачком. В скачке статическое давление потока увеличивается. Если известен угол отклонения потока и давление, то состояние газа за скачком определенно.

Если поток за скачком изоэнтропически затормозить, то сост-е полного торможения харак-ся точкой, в кот-й легко находится значение p. Если предоставить теперь потоку возм-сть изоэнтропически расшириться до давления перед скачком, то его состояние будет определено точкой Е2. Скорость газа при этом может быть вычислена по урав. энергии: (ккал/кг)

где H02 — изоэнтропический перепад энтальпий за скачком. Величину H02 можно рассматривать как сумму Hо2=Н0к + Hon

где Н0к — кинетическая энергия потока за скачком:

Н0п — изменение потенциальной энергии потока в скачке.

При обтекании тела сверхзвуковым потоком перед телом возникает ударная волна (скачок уплотнения); при переходе через эту волну энтропия газа растет, а скорость уменьшается.

Таким образом, в сверхзвуковом потоке идеальной жидкости появляется особый вид сопротивления — волновое сопротивление, зависящее от потерь в скачках, а следовательно, от формы и интенсивности скачков. Как мы видели, форма скачка и его интенсивность зависят от формы тела и скорости обтекания. Учитывая, что при уменьшении угла отклонения потери в скачке уменьшаются, можно заключить, что остроконечные тела в сверхзвуковом потоке должны обладать меньшим сопротивлением, чем тела, имеющие скругленную форму.

Изменение потерь в скачках в завис-ти от их инт-сти можно проследить в тепловой диаграмме построение „ударной поляры*.

Для расчета скачков оказывается весьма удобным пользоваться специальными диаграммами. Такие диаграммы позволяют легко определить характеристики скачка по двум заданным параметрам.

Дата добавления: 2017-02-01