Услов. толщины и интегр-ое соот-е для погран-го слоя

скорость в пограничном слое u с ростом y асимптотически приближается к значению скорости внешнего потока u0. Величина δ зависит от того, где выбрана точка, условно показывающая границу слоя.

Поэтому в расчетах пограничного слоя вводятся другие интегральные толщины, зависящие от δ: толщина вытеснения δ *‚ толщина потери импульса δ ** и толщина потери энергии δ ***.

Для выяснения физического смысла указанных толщин сравним течение идеальной и вязкой жидкостей около твердой стенки.

При отсутствии трения за единицу времени через поперечное сечение потока высотой dу и шириной, равной единице, протечет масса p0u0dy. В пограничном слое за то же время через сечение dу протечет масса pudy.

Разность этих количеств составит:

Второй интеграл правой части мал по сравнению с первым. Поэтому интегрирование достаточно проводить только в пределах физической толщины слоя δ.

Разделив найденный излишек массы на p0u0, получим:

Величина δ * показывает смещение линии тока в направлении внешней нормали к контуру обтекаемого тела.

Вместе с тем δ * характеризует уменьшение расхода жидкости через сечение слоя, „нормальное“ к стенке, обусловленное „вытеснением“ жидкости пограничным слоем, и поэтому носит название толщины вытеснения.

Толщина потери импульса δ ** равна такой толщине слоя жидкости, движущейся со скоростью u0 вне пограничного слоя, количество движения которой равно импульсу сил трения в пограничном слое. Это количество движения, „потерянное“ в пограничном слое, будет равно:

Разделим полученное выражение на p0uo2. Тогда получим:

Масса жидкости pudy теряет в пограничном слое кинетическую энергию, равную pu(uo2-u2)dy. Для всего слоя эта потеря составит: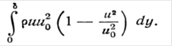

Тогда толщина потери энергии представляет собой толщину движущейся вне слоя жидкости, обладающей кинетической энергией, потерянной в пограничном слое.

39Общее выраж-е д/коэф-та сопрот-ия трения в погран-ом слое при наличии градиента давления

В уравнении импульсов содержатся две искомые пере­менные величины: толщина слоя 6 (или взаимосвязанные условные толщины 8* н 6**) и напряжение трения на стенке т₀.

В общем случае т₀ определяется скоростью на внешней

границе пограничного слоя, ее производными ии", и” и

т. д., характерным размером, например толщиной потери импульса Ь**, плотностью р, температурой Т и коэффици­ентом кинематической вязкости v. Следовательно,

Используя основные положения теории размерности, из функциональной зависимости (5-40) нетрудно получить структурную формулу для коэффициента сопротивления.

Примем в качестве основных размерности скорости «₀, плотности р, длины 8** и температуры Т. Простой про­веркой легко убедиться, что, комбинируя указанные вели­чины, можно получить размерности всех остальных пара­метров. Действительно, х₀ имеет размерность кг/м². Ту же размерность будет иметь и комплекс р и₀: [кг-сек^г1м^А-м²[сек^г\. Следовательно, отношение *„/Ро^ио' представляющее собой местный коэффициент трения c_ft окажется безразмерным. Переходя в выражении (5-40) от размерных величин к безразмерным, получим

Здесь - число Рейнольдса, подсчитанное по толщине потери импульса.

Здесь —число Рейнольдса, подсчитанное

по толщине потери импульса.

Число безразмерных параметров в выражении (5-41) можно сократить, если принять, что напряжение трения определяется так же, как и в случае ламинарного течения только первой производной скорости и.

Дата добавления: 2017-02-01