
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Системы линейных уравнений
|
|
|
|
Определение обратной матрицы; отсутствие обратной матрицы у вырожденной
Пусть А=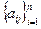
 – квадратная матрица.
– квадратная матрица.
Определение: матрица  называется обратной к матрице А, если выполнено равенство
называется обратной к матрице А, если выполнено равенство 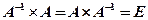 . (5.19)
. (5.19)
Отметим, что вырожденная матрица обратной иметь не может, ибо если detA=0, то из (5.19) и (5.15) имеем: 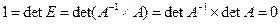 (противоречие).
(противоречие).
5.10 Теорема о существовании обратной матрицы и алгоритм её нахождения
Имеет место следующая теорема:
Всякая невырожденная матрица А=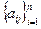
 имеет обратную матрицу
имеет обратную матрицу 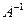 = =
= =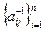
 , элементы которой находят по формуле:
, элементы которой находят по формуле: 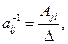 (5.20)
(5.20)
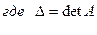 , а
, а 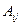 – её алгебраические дополнения.
– её алгебраические дополнения.
Доказательство теоремы:
Пусть 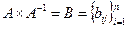
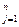 . Тогда:
. Тогда:
(5.20) (5.3)
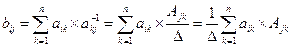 (5.21)
(5.21)
Используем далее 11-е и 12-е свойства определителей (см. §2.2 и §2.3). Если i=j, то
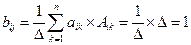 , (5.22)
, (5.22)
ибо последняя сумма является разложением определителя Δ по его i-й строке.
В случае 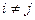 будет
будет  (5.23)
(5.23)
(сумма произведений элементов i-й строки на алгебраические дополнения другой j-й строки 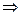 см. 12-е св-во), и тогда
см. 12-е св-во), и тогда 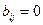 , если
, если 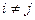 .
.
Сопоставляя (5.22) и (5.23), имеем:  , т.е. В=Е, и теорема доказана.
, т.е. В=Е, и теорема доказана.
Равенство 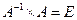 читателю предлагается доказать самостоятельно (в этом случае определитель Δ в равенстве (5.22) будет разлагаться по j-му столбцу).
читателю предлагается доказать самостоятельно (в этом случае определитель Δ в равенстве (5.22) будет разлагаться по j-му столбцу).
Отметим, что определенная формулой (5.20) обратная матрица единственна, ибо если 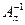 и
и 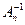 – такие матрицы, что
– такие матрицы, что 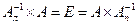 , то
, то 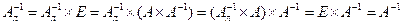 , и
, и
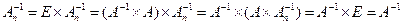 , т.е.
, т.е. 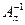 =
=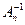 =
=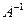 .
.
Покажем также, что
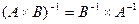 (5.24)
(5.24)
В самом деле: 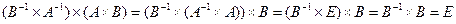 , и (5.24) доказано.
, и (5.24) доказано.
Итак, мы показали справедливость следующих свойств произведений матриц:
1) 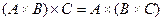 ;
;
2) 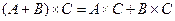 и
и  ;
;
3) 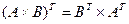 ;
;
4) det(A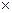 B)=detA
B)=detA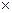 detB;
detB;
5) 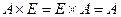 ;
;
6) 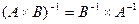 ;
;
7) 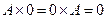 ;
;
8) 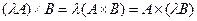 .
.
Свойства 1) ÷ 6) были доказаны ранее.
Свойство 7) очевидно, ибо если 0=В =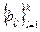
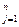 с
с 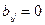 для любых l и j, то для произведения
для любых l и j, то для произведения 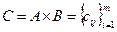
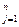 имеем:
имеем:
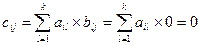 для любых i и j, т.е. С=0.
для любых i и j, т.е. С=0.
Покажем свойство 8):
Пусть А =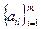
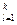 ; В =
; В =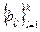
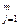 .
.
Тогда произведение 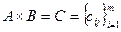
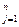 c
c 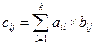 . (5.25)
. (5.25)
Также: 
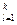 с
с 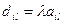 ; (5.26)
; (5.26)

 с
с 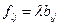 (5.27)
(5.27)
и 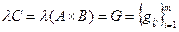
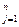 c
c 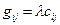 . (5.28)
. (5.28)
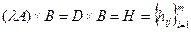
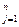 c
c 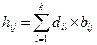 ; (5.29)
; (5.29)

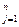 c
c 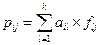 . (5.30)
. (5.30)
Из равенства (5.30) имеем:
(5.27) (5.3) (5.25) (5.28)
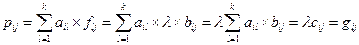 ,
,
(5.28) (5.25) (5.3) (5.26) (5.29)
и 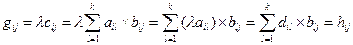 ,
,
т.е. P=G=H, или 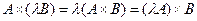 , и свойство 8) доказано.
, и свойство 8) доказано.
Алгоритм нахождения обратной матрицы
Из формулы (5.20), чтобы найти обратную матрицу 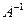 , нужно:
, нужно:
1) найти детерминант матрицы А; если он равен нулю, то обратной нет. Если detA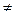 0, то находим
0, то находим
2) матрицу 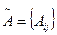 из алгебраических дополнений;
из алгебраических дополнений;
3) транспонируем эту матрицу 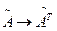 ;
;
4) всякий элемент матрицы 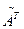 делим на detA, получим матрицу
делим на detA, получим матрицу 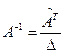 .
.
Рассмотрим пример: Пусть 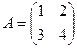 . Найдем обратную матрицу
. Найдем обратную матрицу 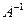 :
:
1) detA = –2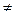 0;
0;
2) дополнения: 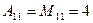 ;
; 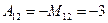 ;
; 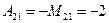 ;
; 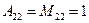 и
и 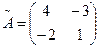 ;
;
3) 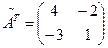 ;
;
4) 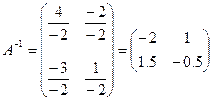 .
.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 458; Нарушение авторских прав?; Мы поможем в написании вашей работы!