
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ранг матрицы
|
|
|
|
Рассмотрим матрицу А размера m  n.
n.
A= 
Выделим в ней k строк и k столбцов (k≤ min (m,n)). Из элементов стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются минорами этой матрицы. В матрице А пунктиром выделен минор 2-го порядка.
Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается r, r(A) или rang(A).
Очевидно, что 0≤ r≤ min (m,n), где min (m,n)- меньшее из чисел m и n.
Минор, порядок которого определит ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.
Пример. Найти ранг матрицы:
А=
Решение. Все миноры 3-го порядка равны нулю. Есть минор 2-го порядка, отличный от нуля.
Значит, rang(A)=2.
 = -9-6=-15 ≠0
= -9-6=-15 ≠0
Базисный минор стоит на пересечении 2 и 3 строки с 1 и 3 столбцами.
Свойства ранга матрицы:
1) При транспонировании матрицы ее ранг не меняется;
2) Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменяется.
3) Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан один из способов вычисления ранга матрицы.
Пример 3.5. Найти ранг матрицы, используя результат примера с пункта 1.3.
А= 
Решение:
А ~  - Канонический вид матрицы А.
- Канонический вид матрицы А.

А ~ Таким образом, ранг матрицы А равен rang(A)=2.
Таким образом, ранг матрицы А равен rang(A)=2.
3.5. Решение матричных уравнений.
Рассмотрим матричное уравнение А  Х=В, где А =
Х=В, где А = 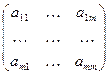 , Х=
, Х=  :, В=
:, В= 
Умножим обе части уравнения на обратную матрицу:
А-∙1А Х=А-1∙В
Х=А-1∙В
Воспользовавшись определением матрицы, получим:
Е∙Х= А-1∙В, т. к. А∙А-1=Е
Вспомним свойства операций над матрицей, тогда имеем: Х=А-1*В, таким образом, мы получим решение матричного уравнения.
Следовательно, для нахождения Х, если известны А и В, надо:
1) найти А-1;
2) умножить А-1 на В.
Пример. Решить уравнение А∙Х=В.
А=  ; В=
; В=  ; Х=А-1∙В
; Х=А-1∙В
Найдем А-1; а) det(A)
б) А11=-2; А12=4; А13=1; А21=0; А22=-2; А23=1; А31=2; А32=-2; А33=-1
в)
А=  ;
;
г) АТ= ;
;
д) А-1=
2) Найдем Х=А-1∙В;
Х= ∙
∙ =
=
3) Проверка: А  Х=В
Х=В  ∙
∙  =
=
Задания для самостоятельной работы №237. Проверочная работа
Решить матричное уравнение.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 381; Нарушение авторских прав?; Мы поможем в написании вашей работы!