Точка перетину прямої і площини

Нехай пряму (l) задано канонічними рівняннями

,

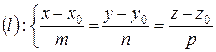площину (Р) задано загальним рівнянням

(Р): .

В цьому випадку доцільно переписати рівняння прямої в параметричній формі (3.21):

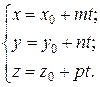
Точка 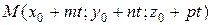лежить на прямій (l), при будь-яких значеннях t є поточною точкою прямої. Спільним точкам прямої і площини відповідають ті значення t, при яких координати точки М задовольняють рівняння площини. Для відшукання таких значень підставимо координати точки М у рівняння площини:

.

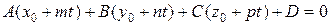Розкривши дужки і згрупувавши члени, одержимо:

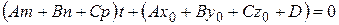. (3.29)

Розглянемо існуючі можливості.

а) (нагадаємо, що згідно з (3.27) це означає, що пряма (l) не паралельна площині (Р). В цьому випадку рівняння (3.29) має єдиний розв’язок

,

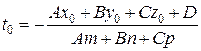а точка є спільною точкою прямої (l) і площини (Р), тобто точкою їх перетину.

б) 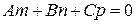, , тобто згідно з (3.27) пряма (l) паралельна площині (Р), але не лежить у цій площині, тому що координати точки прямої 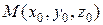не задовольняють рівняння площини. Рівняння (3.29) у цьому випадку приймає вигляд

,

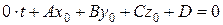і не має розв’язків, бо . Пряма та площина не мають точки перетину.

в) 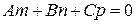, 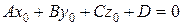. Це означає, що пряма паралельна площині, а точка прямої 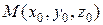лежить у площині, отже і вся пряма (l) лежить у площині (Р). Рівняння (3.29) в цьому випадку має вигляд

,

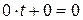і задовольняється будь-якими значеннями t (має безліч розв’язків).

Приклад 1. Знайти точку перетину прямої

і площини

.

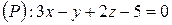Розв’язання. Пряму (l) задано канонічними рівняннями. Перепишемо їх у параметричній формі

; ;

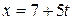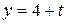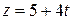
і підставимо ці вирази в рівняння площини, щоб визначити при якому значенні t координати точки прямої задовольняють рівняння площини.

.

Розкриємо дужки і зведемо подібні члени:

, звідки t = –1.

Підставляючи це значення у параметричні рівняння прямої, одержимо

; ; .

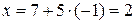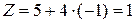Отже, пряма (l) перетинає площину (Р) в точці .

Приклад 2. Чи лежить пряма

у площині

?

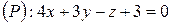Розв’язання. Очевидно, що для належності прямої (l) до площини (Р) необхідно виконання двох умов:

а) ортогональність напрямного вектора прямої 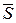і нормального вектора площини ;

б) належність хоча б однієї точки прямої до цієї площини.

Перевіримо виконання цих умов.

а) , , отже 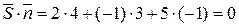, тобто .

б) Координати беремо з канонічних рівнянь прямої: 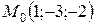. Підставляємо в рівняння площин:

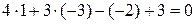; 0 = 0.

Ми одержали вірну рівність, отже .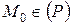

Таким чином пряма (l) лежить у площині (Р).

Дата добавления: 2014-01-04