Кут між двома прямими

1. Задано дві прямі (l ₁) і (l ₂). Потрібно обчислити кут між ними. Розглянемо два випадки, які відрізняються способом завдання прямих.

а) Прямі задані загальними рівняннями:

(l ₁): А ₁ х + В ₁ у + С ₁ = 0;

(l ₂): А ₂ х + В ₂ у + С ₂ = 0.

Рис. 3. 13

З цих рівнянь маємо координати нормальних векторів прямих: = (А ₁; В ₁) і = (А ₂; В ₂), і кут між прямими можна знайти як кут між площинами у п.3.4 (рис. 3.13):

cos (l ₁ˆ l ₂) = cos |(ˆ)| = = (3.37)

Умовою паралельності прямих є паралельність їх нормальних векторів, тобто пропорціональність координат цих векторів:

((l ₁)║(l ₂)) Û (║) Û 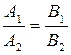. (3.38)

Умовою перпендикулярності прямих є умова ортогональності їх нормальних векторів:

((l ₁)^(l ₂)) Û (^) Û (×= 0) Û A ₁ A ₂ + B ₁ B ₂ = 0. (3.39)

б) Прямі задані канонічними рівняннями:

(l ₁): ;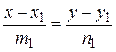

(l ₂): .

З цих рівнянь маємо координати напрямних векторів прямих: 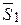= (m ₁; n ₁) і = (m ₂; n ₂), і кут між прямими можна знайти як у п.3.6:

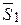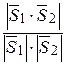cos (l ₁ˆ l ₂) = cos |(ˆ)| = = (3.40)

Умовою паралельності прямих є паралельність їх напрямних векторів, тобто пропорціональність координат цих векторів:

((l ₁)║(l ₂)) Û (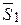║) Û . (3.41)

Умовою перпендикулярності прямих є умова ортогональності їх нормальних векторів:

((l ₁)^(l ₂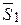)) Û (^) Û (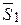×= 0) Û m ₁ m ₂ + n ₁ n ₂ = 0. (3.42)

в) Прямі задані рівняннями з кутовим коефіцієнтом:

Рис. 3. 14

(3.43)

Тоді k ₁ = tg α ₁, k ₂ = tg α ₂, де α ₁ і α ₂ – відповідно кути нахилу прямих (l ₁) і (l ₂) до осі Ох (рис. 3.14). Знайдемо тангенс кута між прямими:

tg (l ₁ˆ l ₂) = tg (α ₂ – α ₁) =

=.

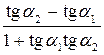
В загальному випадку

tg (l ₁ˆ l ₂) = 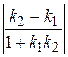. (3.44)

Умова паралельності очевидна: α ₁ = α ₂, звідки tg α ₁ = tg α ₂, отже

k ₁ = k ₂. (3.45)

Умову перпендикулярності одержимо, переписавши рівняння (3.43) як загальні і скориставшись умовою (3.39) (де , , ):

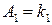k ₁ k ₂ + 1 =0, звідки . (3.46)

Приклад 1. Знайти точку перетину двох прямих

(l ₁): 5 х – 2 у + 16 = 0;

(l ₂): 3 х + у + 3 = 0.

Розв’язання:

Згідно з формулою (3.3) координати точки перетину, як спільної точки прямих (l ₁) і (l ₂) двох прямих, повинні задовольняти рівняння обох прямих, отже вони є розв’язком системи рівнянь:

Розв’язуючи цю систему, одержуємо х = –2; у = 3. Отже прямі (l ₁) і (l ₂) перетинаються в точці М (-2;3).

Приклад 2. Написати рівняння прямої (l ₁), яка проходить через точку М ₀(х ₀; у ₀) паралельно до заданої прямої (l).

Розв’язання:

а) Нехай пряму (l) задано загальним рівнянням

(l): 5 х – 2 у + 16 = 0, М ₀(2;–3).

З рівняння прямої (l) знаємо її нормальний вектор = (5;–2). Оскільки шукана пряма (l ₁)║(l), то її нормальний вектор ║. Не обмежуючи загальності, можна взяти = = (5;–2). Залишається скористатись рівнянням прямої за точкою і нормальним вектором (3.31):

5(х – 2) – 2(у +3) = 0 або 5 х – 2 у – 16 = 0.

б) Нехай пряму (l) задано рівнянням з кутовим коефіцієнтом:

(l): у = 3 х – 2, М ₀(–2;1).

Задана пряма (l) має кутовий коефіцієнт k = 3. Оскільки шукана пряма (l ₁)║(l), то її кутовий коефіцієнт k ₁ = k = 3. скориставшись рівнянням прямої за точкою і кутовим коефіцієнтом (3.36), маємо відповідь

(l ₁): у – 1 = 3(х + 2), або у = 3 х + 7.

Приклад 3. Написати рівняння прямої (l ₁), яка проходить через точку М ₀(х ₀; у ₀) перпендикулярно до заданої прямої (l).

Розв’язання:

а) Нехай пряму (l) задано загальним рівнянням

(l): 3 х + 4 у – 11 = 0, М ₀(2;6).

Нормальний вектор прямої (l) = (3;4). Оскільки шукана пряма (l ₁)^(l), то її напрямний вектор ║. Можемо взяти == (3;4). Тоді рівняння шуканої прямої (l ₁) запишеться як рівняння прямої за точкою і напрямним вектором (3.32):

(l ₁): , або 4 х – 3 у + 10 = 0.

б) Пряму (l) задано рівнянням з кутовим коефіцієнтом:

(l): у = –2 х + 5, М ₀(3;–1).

Задана пряма (l) має кутовий коефіцієнт k = –2. Шукана пряма (l ₁)^(l), тому її кутовий коефіцієнт згідно з умовою перпендикулярності (3.46) дорівнює 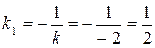. Рівняння шуканої прямої (l ₁) одержимо тепер як рівняння прямої за точкою і кутовим коефіцієнтом (3.36):

(l ₁): у + 1 = 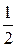(х – 3), або х – 2 у – 5 = 0.

Приклад 4. Знайти кут між прямими (l ₁) і (l ₂).

Розв’язання:

а) Прямі задано загальними рівняннями:

(l ₁): 2 х – у + 8 = 0;

(l ₂): 6 х + 2 у – 7 = 0.

Нормальні вектори прямих відповідно = (2;–1) і = (6;2). Кут між прямими знаходимо як кут між їх нормальними векторами за формулою (3.37):

cos (l ₁ˆ l ₂) = = = = .

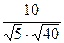Отже кут

(l ₁ˆ l ₂) = arccos= = 45°.

б) Прямі задано рівняннями з кутовими коефіцієнтами:

(l ₁): у = – 3 x + 5;

(l ₂): у = – x – 2.

Кутові коефіцієнти прямих відповідно k ₁ = –3, k ₂ = –1. За формулою (3.44)

tg (l ₁ˆ l ₂) = = = = .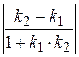

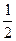Отже кут

(l ₁ˆ l ₂) = arctg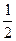» 26°34¢.

Дата добавления: 2014-01-04