
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Еліпсоїд
|
|
|
|
Канонічні рівняння алгебраїчних поверхонь другого порядку
 Означення. Еліпсоїдом називається поверхня, яка в деякій декартовій системі координат має канонічне рівняння вигляду
Означення. Еліпсоїдом називається поверхня, яка в деякій декартовій системі координат має канонічне рівняння вигляду
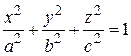 , (3.58)
, (3.58)
де а, b, с – додатні числа, які називаються півосями еліпсоїда.
Основні властивості еліпсоїда, які випливають з його канонічного рівняння, можна встановити міркуваннями, подібними до проведених у п. 3.10:
1. Еліпсоїд є алгебраїчною поверхнею другого порядку.
2. Площини О xy, О xz, О yz є площинами симетрії еліпсоїда, а початок координат – центром симетрії.
3. Еліпсоїд – обмежена поверхня, тому що 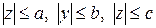 .
.
4. Еліпсоїд перетинає осі координат у точках 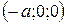 ,
, 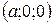 ,
, 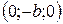 ,
, 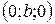 ,
, 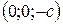 і
і 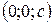 . Ці точки називаються вершинами еліпсоїда.
. Ці точки називаються вершинами еліпсоїда.
Для уточнення вигляду еліпсоїда застосуємо метод перерізів, який полягає у розгляді ліній перетину даної поверхні площинами, паралельними координатним площинам О xy, О xz, О yz.
Розглянемо перерізи даного еліпсоїда площинами, паралельними площині О xy. Рівняння такої площини має вигляд 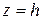 , а лінія, яку одержимо в перерізі, визначається рівняннями
, а лінія, яку одержимо в перерізі, визначається рівняннями
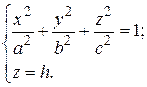
Підставимо 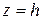 у рівняння еліпсоїда:
у рівняння еліпсоїда:
 , або
, або
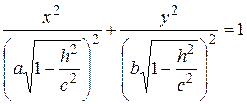 ,
,
тобто одержуємо рівняння еліпса з півосями 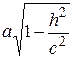 і
і 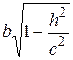 . При
. При  маємо еліпс з півосями а і b, при зростанні
маємо еліпс з півосями а і b, при зростанні 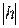 його півосі зменшуються, і при
його півосі зменшуються, і при 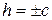 стануть рівними нулю, тобто еліпс вироджується в точку. При
стануть рівними нулю, тобто еліпс вироджується в точку. При  площина
площина 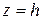 не перетинає еліпсоїду. Перерізи еліпсоїда площинами
не перетинає еліпсоїду. Перерізи еліпсоїда площинами  і
і 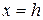 дають аналогічні результати.
дають аналогічні результати.
Якщо дві півосі однакові, наприклад 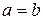 , то в перерізі площинами
, то в перерізі площинами 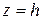 отримуємо не еліпси, а кола. Тоді замість трьохосьового еліпсоїда маємо еліпсоїд обертання – поверхню, одержану обертанням еліпса навколо осі симетрії О z. Якщо еліпс обертається навколо великої осі, одержуємо витягнутий еліпсоїд, якщо навколо малої – сплющений.
отримуємо не еліпси, а кола. Тоді замість трьохосьового еліпсоїда маємо еліпсоїд обертання – поверхню, одержану обертанням еліпса навколо осі симетрії О z. Якщо еліпс обертається навколо великої осі, одержуємо витягнутий еліпсоїд, якщо навколо малої – сплющений.
Якщо ж усі три півосі рівні між собою, то еліпсоїд перетворюється на сферу.
2. Однополий гіперболоїд.
Означення. Однополим гіперболоїдом називається поверхня, яка в деякій декартовій системі координат має канонічне рівняння вигляду
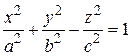 , (3.59)
, (3.59)
де а, b, с – додатні числа, які називаються півосями гіперболоїда.
З рівняння (3.59) випливає:
1. Однополий гіперболоїд є алгебраїчною поверхнею другого порядку.
2. Площини О xy, О yz, O xz є площинами симетрії, а початок координат – центром симетрії гіперболоїда.
3. Вершини гіперболоїда – точки його перетину з осями координат 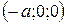 ,
, 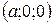 ,
, 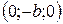 ,
, 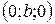 . Вісь О z він не перетинає.
. Вісь О z він не перетинає.
Переріз однополого гіперболоїда площиною 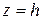 дає:
дає:
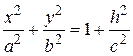 , або
, або
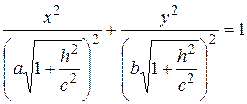 , (3.60)
, (3.60)
тобто еліпс з півосями 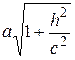 і
і 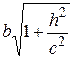 . При
. При  півосі цього еліпса дорівнюють а і b, при необмеженому збільшенні
півосі цього еліпса дорівнюють а і b, при необмеженому збільшенні 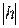 ці півосі теж необмежено зростають. Переріз площиною
ці півосі теж необмежено зростають. Переріз площиною 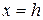 являє собою гіперболу
являє собою гіперболу
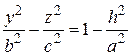 , або
, або
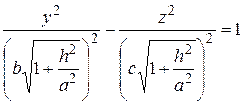 при
при 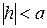 ,
,
і гіперболу
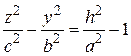 , або
, або
 при
при 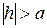 .
.
Якщо ж 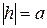 , то в перерізі отримуємо
, то в перерізі отримуємо
 , або
, або 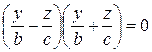 ,
,
тобто пару прямих, які перетинаються:
 і
і 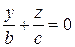 .
.
Аналогічну картину одержимо при перерізі однополого гіперболоїда іншими площинами, паралельними осі O z (рис. 3.21).
 На підставі розглянутих перерізів доходимо висновку, що однополий гіперболоїд має вигляд нескінченої трубки, яка необмежено розширюється в обидва боки в міру віддалення від площини O хy і “зіткана” з прямих ліній, які лежать у площинах, паралельних осі O z.
На підставі розглянутих перерізів доходимо висновку, що однополий гіперболоїд має вигляд нескінченої трубки, яка необмежено розширюється в обидва боки в міру віддалення від площини O хy і “зіткана” з прямих ліній, які лежать у площинах, паралельних осі O z.
Ці прямі лінії називаються прямолінійними твірними однополого гіперболоїда.
У випадку а = b рівняння (3.60) визначають коло з центром на осі O z, і ми маємо однополий гіперболоїд обертання, тобто поверхню, одержану обертанням гіперболи навколо її уявної осі.
3. Двополий гіперболоїд.
Означення. Двополим гіперболоїдом називається поверхня, яка в деякій декартовій системі координат має канонічне рівняння вигляду
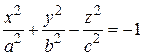 , (3.61)
, (3.61)
де а, b, с – додатні числа, які називаються півосями гіперболоїда.
Основні властивості двополого гіперболоїда:
1. Двополий гіперболоїд є алгебраїчною поверхнею другого порядку.
2. Площини О xy, О yz, О хz є площинами симетрії, а початок координат – центром симетрії гіперболоїда.
3. Вершини гіперболоїда – точки його перетину з віссю О z 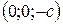 ,
, 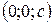 . Осі О х і О y він не перетинає.
. Осі О х і О y він не перетинає.
 Переріз площиною
Переріз площиною 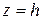 дає еліпс з півосями
дає еліпс з півосями 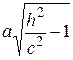 і
і 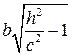 , отже при
, отже при 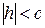 перетину немає, при
перетину немає, при 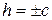 одержуємо точку, а при подальшому збільшенні
одержуємо точку, а при подальшому збільшенні 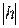 – еліпс, розміри якого зростають необмежено при необмеженому зростанні
– еліпс, розміри якого зростають необмежено при необмеженому зростанні 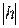 . Лінії перетину з площинами
. Лінії перетину з площинами 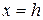 і
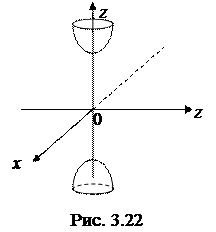
і  – гіперболи. Із сказаного випливає, що двополий гіперболоїд є поверхня, яка складається з двох окремих “порожнин” (дві поли), кожна з яких має вигляд нескінченної опуклої чаші (рис. 3.22).
– гіперболи. Із сказаного випливає, що двополий гіперболоїд є поверхня, яка складається з двох окремих “порожнин” (дві поли), кожна з яких має вигляд нескінченної опуклої чаші (рис. 3.22).
У випадку а = b отримуємо двополий гіперболоїд обертання, утворений обертанням гіперболи навколо дійсної осі.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 5922; Нарушение авторских прав?; Мы поможем в написании вашей работы!