Відношення

Еліпс.

Алгебраїчні лінії другого порядку

Означення. Еліпсом називається множина точок площини, сума відстаней яких від двох заданих точок цієї площини (які називаються фокусами еліпса) є величина стала.

Рис. 3. 15

Нехай точки F ₁ і F ₂ – фокуси еліпса, а М – його довільна точка. Тоді сума довжин F ₁ М і F ₂ М є величина стала для даного еліпса, позначимо її через 2 а: F ₁ М + F ₂ М = 2 а. Відстань F ₁ F ₂ між фокусами еліпса позначимо 2 с, очевидно с < а. Оберемо систему координат таким чином, щоб вісь Ох проходила через фокуси, а початком координат була середина відрізка F ₁ F ₂ (рис. 3.15). Тоді координати фокусів еліпса будуть F ₁(- с; 0), F ₂(с; 0). Координати поточної точки еліпса М позначимо (х; у). За формулою відстані між двома точками

F ₁ М =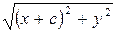, F ₂ М =.

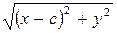Згідно з означенням еліпса точка М (х; у) належить до даного еліпса тоді і тільки тоді, якщо

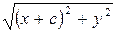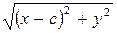+ = 2 а. (3.47)

По суті це і є рівняння еліпса, але щоб переконатися, що перед нами алгебраїчна лінія 2 порядку, проведемо кілька перетворень.

Перенесемо другий радикал у праву частину і піднесемо обидві частини до квадрату:

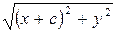= 2 а –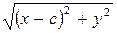

(х + с)² + у ² = 4 а ² – 4 а 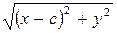+ (х – с)² + у ²

х ² + 2 сх + с ² + у ² = 4 а ² – 4 а 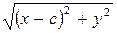+ х ² –2 сх +с² + у ²

4 а 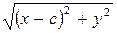= 4 а ² – 4 сх

а 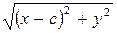= а ² – сх.

Знову піднесемо обидві частини до квадрату і проведемо спрощення:

а ² (х ² –2 сх +с² + у ²) = а ⁴ – 2 а ² сх + с² х ²

(а ² – с²) х ² + а ² у ² = а ²(а ² – с²).

Позначимо а ² – с² = b ² (а ² – с² > 0, бо с < а) і поділимо обидві частини рівняння почленно на а ² b ²:

. (3.48)

Це рівняння називається канонічним рівнянням еліпса. Можна довести, що воно еквівалентне рівнянню (3.47).

Розглянемо основні властивості еліпса, які випливають з його канонічного рівняння.

1. Еліпс є алгебраїчною лінією другого порядку.

2. Якщо точка М (х; у) належить до еліпса, то і точки М ₁(– х; у), М ₂(х; – у), М ₃(– х; – у) теж належать до еліпса (тому що координати х і у входять у рівняння еліпса в парному степені). Це означає, що осі Ох і Оу є осями симетрії еліпса, а точка їх перетину – центром симетрії (рис. 3.15).

3. Оскільки 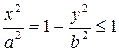і , то , , тобто еліпс – обмежена лінія.

4. Еліпс перетинає вісь абсцис у точках (– а;0) і (а;0), а вісь ординат – у точках (0; b) і (0;– b). Ці точки називаються вершинами еліпса. Величини а і b називаються відповідно великою і малою півосями еліпса.

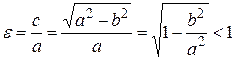(3.49)

називають ексцентриситетом еліпса. Ексцентриситет характеризує ступінь сплюснутості еліпса. Якщо e ® 0, то b ® а, і ми одержуємо рівняння кола радіуса а:

або х ² + у ² = а ²,

тобто коло можна розглядати як граничний випадок еліпса з нульовим ексцентриситетом. Якщо e ® 1, то це означає, що b ® 0, тобто еліпс сплющується до відрізка [ – а; а ].

Прям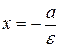і і , паралельні осі Оу, називають директрисами еліпса. Якщо позначимо через r ₁ і r ₂ відстані будь-якої точки еліпса від фокусів, а через d ₁ і d ₂ – відстані тієї ж точки від відповідних директрис (рис. 3.15), то мають місце рівності

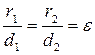. (3.50)

Рівності (3.50) є визначальними для еліпса, тобто еліпс можна визначити як множину точок площини, відношення відстані яких від даної точки (фокуса) до відстані від даної прямої (директриси) є стала величина e Î(0;1).

Відношення 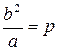називається фокальним параметром еліпса. Легко бачити, що еліпс повністю визначається значеннями параметра p і ексцентриситету e.

Справді

, звідки

, , тобто а і с однозначно виражаються через p і e. Зазначимо, що відстань від фокуса до відповідної директриси дорівнює .

Рівняння

(3.51)

є рівнянням еліпса, центр якого міститься в точці .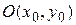

Дата добавления: 2014-01-04