Парабола

Означення. Параболою називається множина всіх точок площини, відстань яких від даної точки (фокуса) дорівнює відстані від даної прямої (директриси), що не проходить через фокус і лежить у тій же площині.

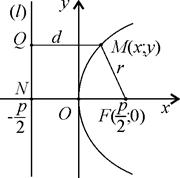Нехай точка F – фокус, а пряма (l) – директриса параболи (рис. 3.18). Відстань FN від фокуса до директриси позначимо р. Величину р називають фокальним параметром параболи.

Рис. 3. 18

Проведемо вісь Ох через фокус F перпендикулярно до директриси (l), а за початок координат оберемо середину відрізка FN. Тоді координати фокуса F (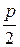; 0), а рівняння директриси (l): х = –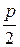. Координати поточної точки М параболи позначимо (х; у), її відстань від директриси QM = d і відстань від фокуса FM = r. Точка М належить до даної параболи тоді і тільки тоді, коли r = d. Виражаючи r і d через координати, одержимо рівняння

.

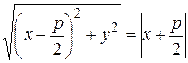Піднесемо обидві частини до квадрата:

х ² – рх + 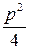+ у ² = х ² + рх + ,

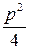звідки

у ² = 2 рх. (3.57)

Це і є канонічним рівнянням параболи.

Виходячи з цього рівняння, розглянемо основні властивості параболи.

1. Парабола – алгебраїчна лінія другого порядку.

2. Оскільки координата у входить у рівняння (3.57) у парному степені, парабола симетрична відносно осі Ох, яку називають віссю параболи.

3. Розв’язуючи рівняння (3.57) відносно у:

у = ,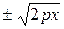

робимо висновок, що парабола визначена тільки для х ≥ 0 (параметр р вважається додатним), тобто лежить у правій півплощині. Рівняння частини параболи, розташованої у першому квадранті має вигляд у = 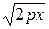. Якщо значення х зростають від 0 до +∞, то відповідні значення у зростають від 0 до +∞, і парабола, відхиляючись від осі Ох, простягається у нескінченність, тобто є необмеженою лінією.

4. Парабола проходить через початок координат О (0; 0), перетинаючи вісь абсцис і дотикаючись до осі ординат. Ця точка називається вершиною параболи.

5. Ексцентриситет параболи, як відношення відстані її точки від фокуса до відстані від директриси, дорівнює 1.

Зауваження. Рівняння у ² = –2 рх також є канонічним рівнянням параболи. Легко встановити, що воно визначає параболу з віссю симетрії Ох, розташовану в лівій півплощині (х ≤ 0) (рис. 3.19, а). Рівняння х ² = 2 ру і х ² = –2 ру визначає параболи з віссю симетрії Оу. Кожна з них дотикається до осі Ох в точці О (0; 0), але перша лежить у верхній півплощині (у ≥ 0) (рис. 3.19, в), а друга в нижній (у ≤ 0) (рис. 3.19, б).

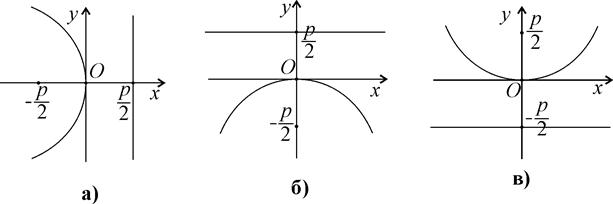
Рис. 3. 19

Рівняння

,

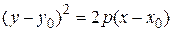так само як і

, , ,

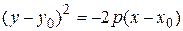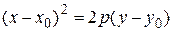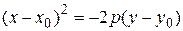визначає параболу, вершина якої міститься в точці .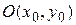

Приклад. Звести до канонічного вигляду рівняння кривої і встановити її тип:

а) 2 х ² + 3 у ² – 4 х + 6 у – 7 = 0;

б) 2 х ² – 3 у ² + 8 х + 18 у – 37 = 0;

в) 4 х ² + 12 х + 3 у – 3 = 0.

Розв’язання. а) Сгрупуємо однойменні змінні та доповнимо вирази в дужках до повних квадратів:

,

,

,

,

.

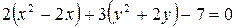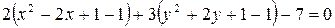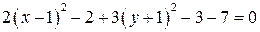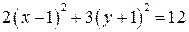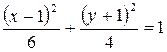Ми отримали рівняння еліпса, центр якого міститься в точці О (1;-1), а півосі дорівнюють: a = 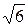; b =2.

б) Як у попередньому прикладі, доповнюємо до повних квадратів:

,

,

,

,

.

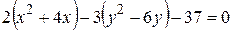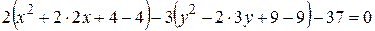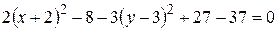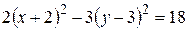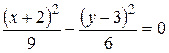Це рівняння гіперболи, центр якої міститься в точці 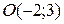, а півосі дорівнюють: a = 3; b =.

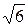в) Доповнюємо до повного квадрата:

,

,

,

;

.

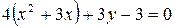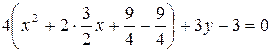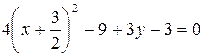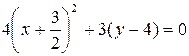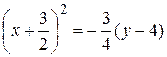Це –рівняння параболи, вершина якої міститься в точці 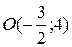, вісь симетрії паралельна осі Оу, а вітки напрямлені вниз (як на рис. 3.19 б)).

Дата добавления: 2014-01-04