Определение 2.1.Число называется пределом функции fв точке а

Предел и непрерывность ФНП.

Окрестность, проколотая окрестность точки

Пусть задана 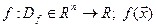и a - предельная точка D_f ó f определена в любой ПО точки
.

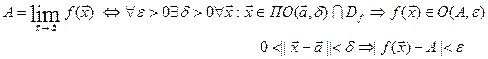
если значения f(x) в точках, “достаточно близких» к а (|| x-a ||<δ) сколь угодно мало отличаются от числа

Замечание. Предел функции в точке существует, если он не зависит от «пути предельного перехода L»: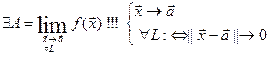

(Для n=1 ФОП: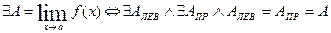

Следствие. Если пределы по двум различным «путям» различны, предел функции в точке НЕ СУЩЕСТВУЕТ!

Например,

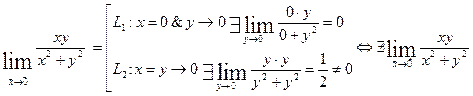
Определение 2.2. Функция называется непрерывной в точке а, если ,

т.е.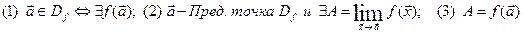

Утверждения.

1) Элементарные функции и их композиции непрерывны в точках области определения.

2) Непрерывная в замкнутой области 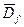(включая точки границы) функция f принимает в точках области все значения от наименьшего “m” до наибольшего “M”, т.е. 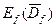=[m;M].

Следствие. АЛГОРИТМ «обобщенного метода интервалов»
решения неравенств f(x,y) >0 / <0 в области непрерывности функции.

(1) Установить и изобразить на плоскости область определения непрерывной функции.
(2) Решить УРАВНЕНИЕ f(x,y) = 0 и изобразить на плоскости соответствующиелинии.

(3) Вычислить значение f( ) в любой “пробной точке” (x,y)^* между соседними линиями и установить таким образом «знак» значений функции в этой области.

Дата добавления: 2014-01-04