Плоскость в пространстве. Уравнение плоскости по точке и нормали. Общее уравнение плоскости и его исследование

Классификация линий второго порядка

I.1.Б

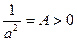
В этом случае уравнение (35.19) выглядит следующим образом

(35.21)

I.1.В A<0; C>0

Тогда, поменяв знаки в обеих частях уравнения (35.19) получим случай I.1.Б.

I.1.Г A<0; C<0

Поменяв в этом случаи знаки в обеих частях уравнения (35.19), мы придем к условию I.1.А.

I.2 F₁≠0

Поделив тогда обе части уравнения (35.18) на F₁, мы получим равенство:

(35.22)

Снова рассмотрим знаки при x² и y² (определяя также коэффициенты a и b).

I.2.А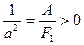

Тогда уравнение (35.22) примет вид

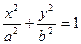(33.4) (это уравнение нам встречалось раннее в §33)

I.2.Б 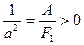; (т.е коэффициент при x² положительный, а при y² отрицательный).

Тогда уравнение (35.22) примет вид

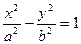(34.1) (а это уравнение нам встречалось в §34)

I.2.В ;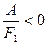

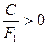
(т.е коэффициент при x² – отрицательный, а при y² – положительный). Тогда, поменяв переменные x и y местами, мы получим случай I.2.Б

I.2.Г ;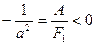

В этом случае уравнение (35.22) принимает вид

, или поменяв в обоих частях последнего уравнения знаки, получим равенство (35.23)

II: A=0; D≠0 (также выполнено условие (35.15))

Тогда уравнение (35.13) принимает вид

(35.24)

В равенстве (35.24) при y₁ выделим полный квадрат

(35.25)

Введем новые переменные

- это соответствует параллельному переносу осей координат.

Тогда уравнение (35.25) примет вид:

, или 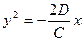(35.26)

Обозначив за , из уравнения (35.26) получим:

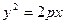(34.3) (это уравнение нами уже рассматривалось в §34)

III: A=D=0

Тогда равенство (35.13) примет вид:

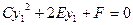(35.27)

Используя такое условие (35.15) или (35.14), выделим в уравнении (35.27) полный квадрат

(35.28)

Введем новые переменные

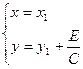
Обозначив далее за , из (35.28) получим

, или (35.29)

Рассмотрим далее следующие случаи:

III.1

Тогда уравнение (35.29) принимает вид:

(35.30)

III.2 В этом случае равенство (35.29) выглядит следующим образом:

(35.31)

III.3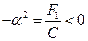

Тогда уравнение (35.29) будет иметь вид:

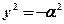(35.32)

Все случаи рассмотрены

Здесь мы рассмотрим все множества на плоскости, координаты всех точек которых задается уравнением второго порядка (35.13)

Ранее было рассмотрены кривые второго порядка:

-Эллипса (уравнение(33.4), с частным случаем эллипса является окружность)

-Гиперболы (уравнение (34.1));

-Параболы (уравнение (34.3))

(собственно говоря, на этом кривые второго порядка исчерпываются, однако остались еще линии второго порядка).

Эти множества можно записать в некоторой системе координат уравнениями (35.20), (35.21), (35.23), (35.30), (35.31) и (35.32).

Определение 35.3 Линией второго порядка называется распадающейся, если она состоит из двух линий первого порядка.

Распадающаяся линия второго порядка задает, например, уравнение (35.21), ибо его можно представить в виде:

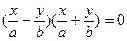, что эквивалентно двум линейным уравнениям:

и 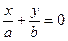(35.33)

А уравнение (35.33) нам задает две пересекающихся прямых линии, проходящих через начало координат.

Таким образом, уравнение (35.21) нам задает пару пересекающихся прямых линий.

Другой пример распадающихся линий – уравнение (35.30), что эквивалентно следующим двум линейным уравнениям.

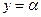, (35.34)

Равенства (35.34) нам задают две параллельные прямые линии (обе эти прямые параллельны на оси абсцисс). Отметим, что всякую пару прямых линий

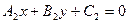можно задать уравнением второго порядка

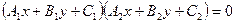
Уравнения (35.21) и (35.30) их канонические уравнения, т.е уравнения в специально подобранной системе координат.

А уравнение (35.31) вообще задает одну прямую линию y=0 (являющейся осью абсцисс)

Отметим также, что всякую прямую линию Ax+By+C=0 можно записать и уравнением второго порядка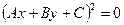

Остальные три уравнения представляют собой вырожденные случаи:

1. Уравнение =0 (35.20)

На плоскости это равенство задает лишь одну точку: x=y=0; координаты никаких других точек на плоскости уравнению (35.20) не удовлетворяют.

Ответим, что всякую точку 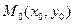на плоскости можно задать следующим уравнением второго порядка:

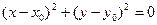
2. Уравнение (35.23)

Ни одна точка на плоскости ему не удовлетворяет, оно задает пустое множество.

Про уравнение (35.23) говорят, что оно задает мнимый эллипс (по аналогии со сходным уравнением(33.2)).

3. Уравнению

Также не удовлетворяет ни одна точка на плоскости, и оно задает пустое множество. По аналогии со сходным ему равенством (35.30) говорят, что уравнение (35.32) задает мнимые параллельные прямые.

Теперь подведем итог:

мы показали, что уравнение второго порядка (35.13) может задавать одно из следующих множеств.

-эллипс (и окружность как частный случай эллипса) кривая второго

-парабола порядка

-гипербола

-две пересекающихся прямые линии распадающиеся линии

-две параллельные прямые линии второго порядка

-одна прямая линия

-одна точка

-пустое множество (мнимый эллипс или мнимые параллельные прямые)

Дата добавления: 2014-01-04