Конус второго порядка

Определение 47.11. Конусом второго порядка называется поверхность, координаты всех точек которой в некоторой системе координат удовлетворяют уравнению

(47.8)

Отметим, что если координаты точки 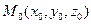удовлетворяют уравнению (47.8), то и для любого действительного t координаты точки 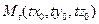также удовлетворяют этому уравнению.

Поэтому, если точка 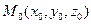лежит на конусе (47.8), то и вся прямая

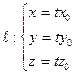(47.32)

(а это – параметрическое уравнение прямой, проходящей через точку 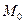и начало координат (см. параграф 42, уравнение (42.2)) также целиком находится на данной поверхности)

Определение 47.12. Эта прямая 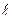называется образующей конуса, а начало координат для уравнения (47.8) будет вершиной конуса.

Общий вид конуса изображён на рис.47.19

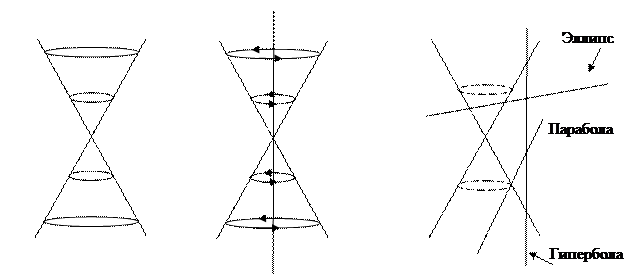
Рис.47.19 Рис.47.20 Рис.47.21

Отметим, что поверхность 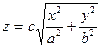(47.33)

(если мы обе части равенства (47.33) возведём в квадрат, затем поделим на 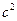и всё перенесём в левую сторону, то получим уравнение (47.8)) является частью конуса (47.8), лежащей выше его вершины, а поверхность

(47.34)

частью конуса (47.8), лежащая ниже его вершины.

Конус (точнее - круговой конус) вращения можно получить, если мы одну из пары пересекающихся прямых (и не перпендикулярных друг другу) будем вращать вокруг другой из них (см. рис. 47.20).

В сечении конуса второго порядка плоскостями могут получиться (см. рис. 47.21 на котором как коническая поверхность, так и все секущие плоскости представлены как вид «сбоку»):

-эллипс (из рис. 47.21 видно, что в сечении конуса второго порядка плоскостью элипс получается некоторая ограниченная кривая второго порядка, т.е. эллипс; может получиться и окружность как частный случай эллипса);

-гипербола (из рис. 47.21 легко получить, что в сечении конуса второго порядка плоскостью гипербола должна быть некоторая разрывная кривая второго порядка, т.е. гипербола);

-парабола (получается в сечении конуса второго порядка плоскостью, параллельной его образующей, исходя из рис. 47.21, читателю предлагается самостоятельно доказать, что в этом случае в сечении должна получиться некоторая неограниченная непрерывная кривая второго порядка, т.е. парабола);

-две пересекающихся прямых линии (получаются в сечении конуса второго порядка плоскостью, проходящей через две его образующих (естественно, эта плоскость должна проходить и через вершину конуса как точку пересечения его образующих));

-одна прямая линия (если плоскость проходит через одну образующую конуса второго порядка, т.е. касается поверхности);

-одна точка (вершина конуса второго порядка; для плоскости, проходящей через вершину конуса выше поверхности и ниже поверхности ).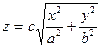

Дата добавления: 2014-01-04