Общее определение конической поверхности

Определение 47.13. Конической называется поверхность, удовлетворяющая следующему свойству

- существует такая фиксированная точка 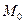, лежащая на поверхности, что для любой точки M, также лежащей на этой поверхности, вся прямая, проходящая через точки M и 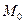, тоже находится на этой поверхности.

Определение 47.14. Точка 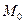в определении 47.13 называется вершиной конуса, а прямая 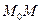из этого же определения носит название образующей конуса.

Определение 47.15. Уравнение 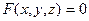(47.35) называется однородным, если из того, что числа 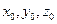удовлетворяют этому уравнению, следует, что и для любого действительного числа t значения 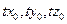также удовлетворяют уравнению (47.35).

Если вершиной конуса является начало координат (что всегда можно сделать, подобрав соответствующим образом оси координат), то из того, что точка 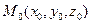удовлетворяет уравнению конической поверхности (т.е. лежит на этой поверхности), следует, что и координаты всей прямой линии 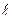, заданной уравнением (47.32), тоже должны удовлетворять уравнению этой поверхности, ибо, согласно определению 47.13, вся прямая 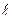, заданная уравнением (47.32), должна лежать на этой конической поверхности. Поэтому в некоторой системе координат уравнение конической поверхности должно быть однородным.

Отметим также, что если точка M лежит на образующей конической поверхности, то и симметричная ей относительно вершины конуса точка также должна находиться на этой же образующей и, следовательно, на данной поверхности. Поэтому всякая коническая поверхность является центральной, а вершина конуса должна быть его центром симметрии.

Задача: доказать, что из всех уравнений перечисленных в конце п.47.1, однородными уравнениями являются лишь (47.8), (35.21), (35.31), (35.20) и (47.7).

Уравнение (47.8) мы уже рассмотрели. Остальные уравнения будут рассмотрены в п.47.7.

Дата добавления: 2014-01-04