Распадающиеся и вырожденные поверхности второго порядка

Осталось рассмотреть множества, заданные уравнениями (35.21), (35.23), (35.30), (35.31), (35.32), (47.7), (47.22) и (35.20)

Определение 47.16. Поверхность второго порядка называется распадающейся, если она состоит из двух поверхностей первого порядка.

В качестве примера рассмотрим поверхность, заданную уравнением

(35.21)

Левую часть равенства (35.21) можно разложить на множители

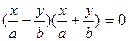(47.36)

Таким образом, точка лежит на поверхности, заданной уравнением (35.21) тогда и только тогда, когда её координаты удовлетворяют одному из следующих уравнений или . А это – уравнения двух плоскостей, которые согласно параграфу 36 (см.п.36.2, 10-ая строка таблицы), проходят через ось аппликат OZ. Следовательно, уравнение (35.21) задаёт распадающуюся поверхность, а точнее – две пересекающихся плоскости.

Задача: Доказать, что если поверхность одновременно является и цилиндрической, и конической, а также состоит более, чем из одной прямой линии, то она распадается, т.е. содержит в себе некоторую плоскость.

Рассмотрим теперь уравнение (35.30)

Его можно разложить на два линейных уравнения и . Таким образом, если точка лежит на поверхности, заданную уравнением (35.30), то её координаты должны удовлетворять одному из следующих уравнений: и . А это, согласно параграфу 36 (см. п.36.2 6-я строка таблицы), является уравнением плоскостей, параллельных плоскости . Таким образом, уравнение (35.30) задаёт две параллельные плоскости и тоже является распадающейся поверхностью.

Отметим, что всякую пару плоскостей и 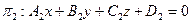можно задать следующим уравнением второго порядка . Уравнения же (35.21) и (35.30) – это канонические уравнения двух плоскостей, то есть их уравнения в специально подобранной системе координат, где они (эти уравнения) имеют наиболее простой вид.

Уравнение же (35.31)

вообще эквивалентно одному линейному уравнению у = 0 и представляет собой одну плоскость (согласно параграфу 36 п.36.2, 12-ая строка таблица, это уравнение задаёт плоскость ).

Отметим, что всякая плоскость можно задать и следующим уравнением второго порядка .

По аналогии с уравнением (35.30) (при ) иногда говорят, что равенство (35.20) задаёт две слившиеся параллельные плоскости.

Переходим теперь к вырожденным случаям.

1.Уравнение 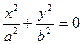(35.20)

Заметим, что точка M(x, y, z) принадлежит множеству, заданному уравнением (35.20), тогда и только тогда, когда её первые две координаты х=у=0 (а её третья координаты z может быть какой угодно). А это означает, что уравнение (35.20) задаёт одну прямую линию – ось аппликат OZ.

Отметим, что уравнение всякое прямой линии 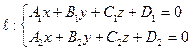(см. параграф 40, п.40.1, а также параграф 37, система (37.3)) можно задать следующим уравнением второго порядка 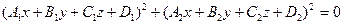. Равенство же (35.20) является каноническим уравнением второго порядка для прямой линии, т.е. её уравнением второго порядка в специально подобранной системе координат, где оно (это уравнение) имеет наиболее простой.

2. Уравнение (47.7)

Уравнению (47.7) может удовлетворять лишь одна тройка чисел x=y=z=0. Таким образом, равенство (47.7) в пространстве задаёт лишь одну точку О (0; 0; 0) – начало координат; координаты никакой другой точки пространства равенству (47.7) удовлетворять не могут. Отметим также, что множество, состоящие из одной точки 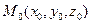можно задать следующим уравнением второго порядка:

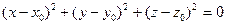
3. Уравнение (35.23)

А этому уравнению вообще не могут удовлетворять координаты никакой точки пространства, т.е. оно определяет пустое множество. По аналогии с уравнением (33.4)

(см. п. 47.5, определением 47.8), его ещё называют мнимым эллиптическим цилиндром.

4. Уравнение (35.32)

Этому уравнению также не могут удовлетворять координаты никакой точки пространства, поэтому и оно определяет пустое множество. По аналогии со сходным уравнением (35.30), эту «поверхность» ещё называют мнимыми параллельными плоскостями.

5. Уравнение (47.22)

И этому уравнению не могут удовлетворять координаты никакой точки пространства, и, следовательно, и оно определяет пустое множество. По аналогии с равенством с равенством (47.17) (см. п. 47.2), это множество ещё называют мнимым эллипсоидом.

Все случаи рассмотрены.

Дата добавления: 2014-01-04